A beteg ember étrendjének legalább 4000 egység vitamint, 50 egység ásványi anyagot és 1400 kalóriát kell tartalmaznia. Két a és B étel kapható egységenként 4 és 3 egység áron. - Matematika
Kérdés Alapértelmezés szerint a megoldások elrejtése
A beteg ember étrendjének legalább 4000 egység vitamint, 50 egység ásványi anyagot és 1400 kalóriát kell tartalmaznia. Két A és B étel kapható egységenként 4, illetve 3 egység áron. Ha egy A egység 200 egység vitamint, 1 egység ásványi anyagot és 40 kalóriát tartalmaz, és egy egység B étel 100 egység vitamint, 2 egység ásványi anyagot és 40 kalóriát tartalmaz, akkor keresse meg, hogy milyen ételkombinációt kell használni a legkevesebb költség?
Megoldás Mutassa meg a megoldást
Hagyja, hogy a beteg x egységet és y egységet vegyen be az étrendből vett I. és II.
Mivel egy élelmiszer egységre az I Rs 4, a II ételé pedig 3 Rs.
Ezért az I élelmiszer x egysége 4x, az y étel II egysége pedig 3y €.
Teljes költség = Rs (4x + 3y)
Jelölje Z a teljes költséget
Ezután Z = 4x + 3y
Ha egy A egység 200 egység vitamint és egy B étel 100 egység vitamint tartalmaz.
Így az I élelmiszer x egysége és a II. Élelmiszer egysége 200x + 100y egység vitamint tartalmaz.
De egy beteg ember étrendjének legalább 4000 egység vitamint kell tartalmaznia.
∴ \ [200x + 100y \ geq 4000 \]
Ha egy A egység 1 egység ásványi anyagot és egy egység B étel 2 egység ásványi anyagot tartalmaz.
Tehát az I élelmiszer x egysége és a II élelmiszer y egysége x + 2y egység ásványi anyagot tartalmaz.
De egy beteg ember étrendjének legalább 50 egység vitamint kell tartalmaznia.
∴ \ [x + 2y \ geq 50 \] Ha egy A egység 40 kalóriát és egy B étel 40 kalóriát tartalmaz.
Tehát az I étel x egysége és a II étel y egysége 40x + 40 év egység kalóriát tartalmaz.
De egy beteg ember étrendjének legalább 1400 kalóriát kell tartalmaznia.
Először a megadott egyenlőtlenségeket konvertáljuk egyenletekké, a következő egyenleteket kapjuk:
200x + 100y = 4000, x + 2y = 50, 40x + 40y = 1400, x = 0 és y = 0
200x + 100y ≥ 4000 által képviselt régió:
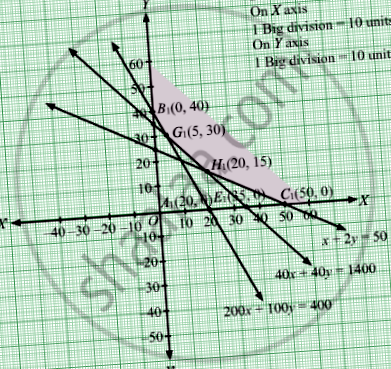
A 200x + 100y = 4000 egyenes megfelel az A1 (20, 0) és a B1 (0,40) koordinátatengelyeknek. Ezen pontok összekapcsolásával megkapjuk az egyeneset
200x + 100y = 4000. Nyilvánvaló, hogy (0,0) nem elégíti ki a 200x + 100y ≥ 4000 egyenletet. Tehát az xy síkbeli régió, amely nem tartalmazza az origót, a 200x + 100y ≥ 4000 egyenlet megoldási halmazát jelenti.
Az x + 2y által képviselt régió ≥ 50:
Az x + 2y = 50 egyenes megfelel a C1 (50, 0) és D1 (0, 25) koordinátatengelyeknek. Ezen pontok összekapcsolásával megkapjuk az egyeneset
x + 2y = 50. Nyilvánvaló, hogy (0,0) nem elégíti ki az x + 2y ≥ 50 értéket. Tehát az a régió, amely nem tartalmazza az origót, az x + 2y ≥ 50 egyenlet megoldási halmazát jelenti.
40x + 40y ≥ 1400 által képviselt régió:
A 40x + 40y = 1400 egyenes megfelel az E1 (35, 0) és az F1 (0, 35) koordinátatengelyeknek. Ezen pontok összekapcsolásával megkapjuk az egyeneset
40x + 40y = 1400. Nyilvánvaló, hogy (0,0) nem felel meg a 40x + 40y ≥ 1400 egyenlőségnek. Tehát az a régió, amely nem tartalmazza az origót, a 40x + 40y ≥ 1400 egyenlet megoldási halmazát jelenti.
Az x ≥ 0 és y ≥ 0 ábrázolt régió:
Mivel az első negyed minden pontja kielégíti ezeket az egyenlőtlenségeket. Tehát az első negyed az a terület, amelyet az x ≥ 0 és y ≥ 0 egyenlőtlenségek képviselnek.
A korlátozások rendszere által meghatározott megvalósítható régió 200x + 100y ≥ 4000, x + 2y ≥ 50, 40x + 40y ≥ 1400, x ≥ 0 és y ≥ 0 a következő.
A célfüggvény értékét ezeken a pontokon az alábbi táblázat adja meg
| Pontok | Z értéke |
| B1 | 4 (0) +3 (40) = 120 |
| G1 | 4 (5) +3 (30) = 110 |
| H1 | 4 (20) + 3 (15) = 125 |
| C1 | 4 (50) +3 (0) = 200 |
A minimális költség 110 Rs, ami G1-nél van (5, 30).
Ennélfogva az étel szükséges kombinációja 5 egység A étel és 30 egység B étel.
- Egész napos fogyókúra terv Vitaminok és ásványi anyagok anyagcsere webáruház
- Ősi ásványi anyagok magnézium fürdő pehely - Ben Greenfield Fitness - Diéta, zsírvesztés és teljesítmény
- Aki Keto-t csinál (enzimek, fogyás, alacsony szénhidráttartalom, vitaminok) - Diéta és fogyás -Súly
- 4 vitamin, amire a diétádnak szüksége van, ha nem tud fogyni - SHEfinds
- 4000 kalóriatartalmú étrend - Hogyan lehet valóban elkészíteni a tornateremben járókat