Az emberi öregedés és a hosszú élettartam hosszú távú tendenciái

Absztrakt

Az elmúlt 200 évben az emberek várható élettartama jelentősen megnőtt. Ezeket az előrelépéseket nagyrészt a környezetük külső javulása (például a rendelkezésre álló étrend, a betegségek előfordulása, az oltás, valamint a higiénia és a higiénia állapota) hajtotta. Ebben a cikkben azt kérdezzük, hogy a várható élettartam jövőbeli javulását felülről korlátozza-e az emberi élettartam. Az élettartamot, szemben a várható élettartammal, a hosszú élettartam biológiai mércéjeként fogalmazzák meg, amelyet a testi romlás belső sebessége vezérel. Kérdésünk megválaszolása érdekében először bemutatjuk a bio-gerontológusok által kidolgozott modern öregedési elméletet, és megmutatjuk, hogy a megváltoztathatatlan élettartam felső korlátot szab a várható élettartamra. Ezután a fejlett országok mintáján megmutatjuk, hogy az így meghatározott emberi élettartam a huszadik század közepéig valóban állandó volt, de azóta nőtt a várható élettartammal szinkronban. Más szavakkal, bizonyítékokat találunk a gyártott élettartamra.

Bevezetés

A közgazdászok számára az emberi élettartam adott állandó. Ez a felső határ T hogy az integrál vagy összeg előjel tetejére tesszük, amikor kiszámítjuk a reprezentatív ügynök várható élettartamát. Az élettartam fogalmilag eltér a várható élettartamtól. Bár gyakran tekintjük állandónak a várható élettartamot, amely az egyik időszakról a másikra való túlélés valószínűségétől függ, ez egy "kényelem érdekében" tett feltételezés, mivel a túlélés minden bizonnyal a makrogazdasági környezettől (GDP fő, orvosok négyzetkilométerenként stb.) és az egyes gazdasági döntésekről (táplálkozás, egészségügyi kiadások stb.).

Míg a közgazdasági elmélet nagy része egyszerűsítő feltételezéseken alapszik, amelyek vagy az élet végéig fennmaradó bizonyos túlélés, vagy az élet időegységenként adott életkorral nem összefüggő túlélési valószínűsége (Yaari 1965 és Blanchard 1985 alapján), létezik még egy, a gazdag irodalom, amely megpróbálja endogenizálni a túlélést és empirikusan elfogadható túlélési valószínűségeket beépíteni a gazdasági érvelésbe. Legjobb tudásunk szerint azonban a közgazdaságtan területén nem végeznek kutatásokat az emberi életre vonatkozóan. 1. lábjegyzet

A várható élettartammal szemben, amely a népességre és a helyzetre jellemző, az élettartamot általában a-ként fogják fel fajspecifikus jellegzetes (Arking 2006; Gavrilov és Gavrilova 1991). Az egerek populációjának várható élettartama például a vadon vagy a laboratórium sajátos környezetétől függ. Az egerek élettartama ezzel szemben független az ilyen körülményektől, de eltér a gyümölcslégyek vagy elefántok élettartamától. Hasonlóképpen, egy adott emberi populáció várható élettartama országonként (Anglia vs. Uganda) és idővel (Anglia ma vs. 200 évvel ezelőtt) eltérő. Az emberi élettartamnak azonban, ha létezik, változatlanul változatosnak kell lennie a populációk között. Valószínűleg minden biológus egyetért az élettartam ezen elképzelésével. De az élettartam méréséről - ellentétben a várható élettartammal - kevésbé könnyű megállapodni.

Az emberi élettartam meghatározása a halálozáskor elérhető maximális életkorként, amint azt számos általános szótár és sok régebbi biológiai közlemény javasolja, minden bizonnyal félrevezető (Wilmoth 1999; Carey 2003). Fogalmilag ezt az elképzelést cáfolja az a belátás, hogy „bármilyen öregek is vagyunk, annak valószínűsége, hogy a következő órán belül meghalunk, soha nem egyenlő az eggyel” (Jacquard 1982). Empirikusan cáfolta az a megfigyelés, hogy a halálozás maximális életkora legalább 140 éve folyamatosan növekszik (Wilmoth és Robine 2003).

Az az egyszerű tény, hogy a valaha a földön élők „mintanagysága” folyamatosan növekszik, arra számíthat, hogy az idő előrehaladtával a maximálisan megfigyelt élethossz növekedni fog. Ezt lenyűgözően mutatja Finch és Pike (1996). Meghatározzák az élettartamot T mint egy populáció utolsó túlélőjének becsült halálozási kora úgy, hogy \ (S (x) = 1/N \) annak valószínűsége, hogy az utolsó ember álljon ki N. Dugaszolás 1 /N empirikusan becsült gompertzi túlélési függvénybe 105 év élettartamot nyernek \ (N = 10 ^ 3 \) és 114 évet \ (N = 10 ^ 7 \). Általánosságban elmondható, hogy a maximumok mintanagyságtól való függése jól ismert tény a szélsőséges értékek statisztikájában (Gumbel 1958).

Ezekből a megfigyelésekből világossá kell válnia, hogy az élettartam, szemben a várható élettartammal, nem határozható meg pusztán statisztikai mérőszámként, biológiai alapok nélkül. Szükségünk van némi megértésre az öregedés biológiai mechanizmusáról annak megállapításához, hogy egy belső mechanizmus, amely szabályozza a testünk romlásának ütemét. A modern biológiában alkalmazott általános érvelést követve, az öregedést és a halált sztochasztikus folyamatnak tekintve (Arking 2006), arra vagyunk kíváncsiak, hogy létezik-e olyan szabályszerűség, amely minden ember számára közös a környezeti és genetikai jellemzőktől függetlenül. Ebből a szabályszerűségből, ha létezik, megpróbáljuk az élettartamot nem abszolút maximumként, hanem az élet jellegzetes hosszaként következtetni. 2. lábjegyzet

Az emberi élettartamra való törekvésünket a 2. szakaszban kezdjük két nagyon erős empirikus törvényszerűség bevezetésével, a halálozás Gompertz – Makeham-törvényével és a halálozás kompenzációs hatásával. Ezeket az empirikus törvényszerűségeket elméletileg alátámasztja a megbízhatóság elmélete, amint azt Gavrilov és Gavrilova (1991) és más bio-gerontológusok bemutatták. Ez egy új, elméletileg megalapozott emberi életfelfogás kidolgozásához vezetett. Ezen elmélet lényegét és következményeit a 2.3. Szakaszban vázoljuk fel. A legfontosabb mennyiségi következtetés az, hogy az emberi élettartam a halálozás becsült kompenzációs hatásából következtethető. A 3. szakaszban megmutatjuk, hogy az emberi élettartam, ha megváltoztathatatlan, a túlélési görbe téglalap alakúvá válásához vezet, és így felső határt szabna az emberi élettartam jövőbeli fejlődésének.

A 4. részben megbecsüljük a Gompertz – Makeham egyenlet paramétereit a nemlineáris legkisebb négyzetek módszerével és az életkor-specifikus halálozási arányokra vonatkozó adatokkal a Humán Halandóság Adatbázisából (2010). Ezután a becsült paraméterekkel elemezzük a halálozás és az emberi élet következtetésének kompenzációs hatását. A mintánkban szereplő összes ország esetében a 20. század közepéig időbeli változatlan kompenzáló hatást figyelhetünk meg. A huszadik század második felére bizonyítékokat találunk az emberi élet szekuláris növekedésére. Más szavakkal azt tapasztaltuk, hogy az emberi találékonyság hatékonyan beleavatkozott a természetbe és létrehozta a „gyártott élettartamot” (Carnes és Olshansky 2007). Végül megmutatjuk, hogy a várható élettartam a múlt század második felében nőtt az élettartammal szinkronban. Nagyrészt és egyre nagyobb mértékben élünk tovább, mert a technológiai fejlődés megváltoztatta az öregedést és a testünk bomlását.

Tanulmányunk folytatja Strehler és Mildvan (1960), valamint Gavrilov és Gavrilova (1991) munkáját. Ezekhez a korábbi munkákhoz képest egy nagyobb, több országból álló és sokkal hosszabb időtartamú mintát használtunk. Ez lehetővé tette számunkra, hogy ne csak megerősítsük az időinvariáns kompenzáló hatás (idő-invariáns élettartam) korábbi eredményét a huszadik század közepéig, hanem - a huszadik század végéről származó új adatok alapján - levezethessük a az emberi élettartam világi növekedése. Ez a megállapítás viszont lehetővé tette számunkra, hogy újszerű magyarázatot nyújtsunk a „várható élettartam határainak megszegése” megfigyelésére (Oeppen és Vaupel 2002): az 1970-es évek óta a később született emberek legalább részben hosszabb életre számíthatnak, mert az emberi élet növekszik.

Az emberi élettartam: elmélet

A halandóság Gompertz – Makeham-törvénye

Az emberi élettartam összes elmélete egy nagyon erős empirikus törvényszerűségen, a halandóság Gompertz – Makeham-törvényén alapul. Benjamin Gompertz aktuáriustól (1825) származik, aki megfigyelte, hogy hosszú életszakasz létezik, körülbelül 30 és 90 év közötti életkor, amelyhez az életkor és a halálozás log-lineárisan kapcsolódik. Jelölje \ (\ mu (x) \) a a halandóság ereje, ez a feltételes valószínűséggel meghal az életkorban x adott életkorig fennmaradó túléléssel x. A Gompertz-törvény ekkor formálisan meg van adva \ (\ mu (x) = R \ exp (\ alpha x) \). Figyelembe véve, hogy a halálokok nem mindegyike összefügg életkorral, Makeham (1860) hozzáadott egy állandó értéket, \ (A \ ge 0 \), amely a híres Gompertz – Makeham képletet adja meg:

Figyelembe véve az egyszerűséget és a pontosságot, a Gompertz – Makeham képlet napjainkig a legmegfelelőbb, tömörebb és legáltalánosabban használt öregedési leírás (Olshansky és Carnes 1997). Paramétereit nagy pontossággal becsülik meg, 0,9 feletti \ (R ^ 2 \) értékkel nemcsak az emberek, hanem az olyan különböző fajok esetében is, mint az élesztő, a gyümölcslegyek és a lovak. A becsült együtthatók természetesen nagymértékben különböznek, tükrözve a fajok közötti élettartam nagy eltéréseit (Arking 2006).

A Gompertz – Makeham-törvény felhasználásával és a \ (\ dot S (x)/S (x) = - \ mu (x) \) megoldással feltétel nélküli valószínűséget kapunk az életkor túlélésére. x. Tekintettel arra, hogy \ (S (0) = 1 \), ekv. 2:

Tól től S(x) következtethetünk a várható élettartamra (várható hátralévő élettartamra) az életkorban x mint \ (L (x) = ^ S (a) \ mathrm a/S (x)> \) .

Az elmúlt évszázadban az emberi születéskor várható élettartam több mint 20 évvel nőtt a teljesen fejlett országok többségében (Riley 2001). Érdekes megvizsgálni, hogyan ragadja meg az emberi élettartam ezen hatalmas javulásait a Gompertz – Makeham-törvény. Erre a célra hasznos elkülöníteni a Makeham paramétert A mert tükrözi az életkorral nem összefüggő halandósági erőket, vagyis a háttérhalandóságot (Bongaarts 2005) vagy a külső halálozást (Carnes és Olshansky 2007). Arra számítunk, hogy az életkorral összefüggő betegségek megelőzése, felszámolása vagy gyógyítása megjelenik a betegség változásaiban A. Ezzel szemben az öregedési folyamat bármely előrehaladása az életkorfüggő Gompertz-paraméterek változásában jelenik meg R és α. Amint az az egyenletekből látható. 1. és 2., alacsonyabb R azt jelentené, hogy az emberek jobb egészségben (fiatalkorban) és alacsonyabb állapotban kezdenek α azt jelentené, hogy az öregedési folyamat lassul. Amint azonban a 2.3. Szakasz mutatja, arra számítunk α és R ne változtassanak önállóan, amíg az emberi élettartam megváltoztathatatlan.

Az elmúlt két évszázadban a háttérhalandóság drámai módon csökkent a mai fejlett országokban (Svédország esetében például \ (5,5 \ cdot 10 ^ \) -tól \ (4,8 \ cdot 10 ^ \); Gavrilov és Gavrilova 1991). Val vel A mivel közel nulla, a várható élettartam jövőbeni előrehaladásának az életkor függő halálozás javulásából kell származnia. Más szavakkal, ha a technológiai fejlődés csak a háttérhalandóságot befolyásolhatná, de a testi pusztulás belső arányát nem, akkor a megfigyelt tendencia, hogy a születéskor várható élettartam születési évenként körülbelül 3 hónappal javul (Oeppen és Vaupel 2002), nem lenne fenntartható jövő. Ennek a ténynek az ösztönzésére néhány gerontológus arra a következtetésre jutott, hogy a születéskor várható várható élettartam valószínűleg nem haladja meg a 85 évet (Fries 1980; Carnes és Olshansky 2007). Egy ilyen hipotézis problémája az, hogy - bár a gyakorlatilag nulla háttérhalandóság nem hagy teret a javulásra -, az adatokban (még) nem láthatjuk a várható élettartam lassulását vagy konvergenciáját (Wilmoth 1997, 1999). Ez azt jelenti, hogy a várható élettartam nemrégiben bekövetkezett előrelépésének olyan folyamatból kell származnia, amelyet a Gompertz-paraméterek változása tükröz.

A halálozás kompenzációs hatása

A Gompertz paraméterek α és R, amelyeket nagy pontossággal becsülnek a adott nemi, országonkénti és időbeli különbség. Ez azt jelenti, hogy bár minden ember úgy tűnik, hogy a halálozás általános általános törvénye szerint öregszik, az e törvényt szabályozó konkrét paraméterek nemtől, származástól és időtől függenek. Továbbá, R és α Úgy tűnik, hogy a földrajztól is függ, és hajlamosak esni (a R) vagy emelkedik (a α) a gazdasági fejlődéssel. Stabilitása miatt a Gompertz-paraméterek önmagukban nem alkalmasak az emberi életidő azonosítására.

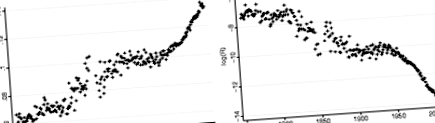
A Gompertz-paraméterek azonban nem változnak egymástól függetlenül, de meglepő módon olyan sajátos módon, hogy megőrzik az inverz asszociációt α és a napló R. Ezt a tényt Strehler – Mildvan-korrelációnak vagy a halálozás kompenzációs hatásának nevezik (Strehler és Mildvan 1960; Gavrilov és Gavrilova 1991). Ábrán Svédország esetében példaértékűen látható. 1. és 2. Az 1. ábra a hosszú távú trendeket mutatja be α és R. Idővel a lejtő paraméter α hajlamos emelkedni és a szint paraméter R hajlamos esni. Ez azt jelenti, hogy az idők folyamán a svéd nők általában gyorsabban öregszenek, de alacsonyabb kezdeti halálozással indulnak. Az alábbiakban bemutatjuk ennek a jelenségnek az általános jellegét az egyes országokban, és hogyan magyarázható az öregedés megbízhatósági elméletében a kezdeti redundancia növekedésével.

A svéd nőstények öregedési tendenciái 1751–2005. Bal oldali panel: Fejlesztése α túlóra. Jobb panel: Fejlesztése R túlóra