4a. Függelék) Grafikus feltáró elemzés (SZÜKSÉGES szkript)

Nathan Brouwer | [email protected] | @lobrowR

2018-12-10

Bevezetés a grafikus adatok feltárásába

Grafikus feltárásra van szükség a minőségellenőrzéshez és az adatok modellezésének megértéséhez. A szerzők egyre többször adják meg a nyers adatok ábráit függelékekben annak érdekében, hogy az olvasók jobban megértsék az adatokat.

Önálló projektjéhez (2018-ban) egyszerűen meg kell adnia egy szkriptfájlt, amely releváns feltáró elemzéseket végez.

Lát Zuur és mtsai 2010 további információért.

Ez a fájl

Ez a fájl áttekintést tartalmaz a legfontosabb adatfeltárási feladatokról. Különösen a regressziós adatokra irányul, de a megbízók általában minden adatra vonatkoznak.

Előzetes

Csomagok betöltése

Adat betöltés

(Megjegyzés: Az eredeti fájlokat az emlalsmilk csomagban „skibiel_mammalsmilk.csv” néven hívják. Az adatokat itt lemásoltuk, de új nevet kaptunk („Függelék-2-Elemzés-Adat_mammalsmilkRA.csv”), hogy ez önálló elemzési összefoglaló legyen. )

Adatok betöltése R-be

Ha telepítette az mammalsmilkRA csomagot, a .csv „Függelék-2-Elemzés-Adatok_emlősökmilkRA.csv” fájl mentésre kerül a mammalsmilkRA R könyvtárba, amely a csomagokkal kapcsolatos fájlok tárolására jött létre. Megtalálhatja a fájl helyét úgy, hogy megkeresi a fájlt a fájlrendszerében (pl. „File Explorer” a Windows rendszerben), majd beállítja a helyét működő könyvtárként, vagy elmenti a fájlt egy kényelmesebb helyre.

Alternatív megoldásként közvetlenül a mammalsmilkRA csomagból töltheti be; a legtöbb elemzést nem csomagolják be, így ez egy egyedi rövidítés, amelyet beállítottam.

Ellenőrizze a bemenetet

Még van egy kis takarítás?

Grafikus feltáró elemzések

A Zuur és mtsai 2010 által vázolt protokollt követem. Az adatok feltárásának protokollja a gyakori statisztikai problémák elkerülése érdekében. Módszerek az ökológiában és az evolúcióban 1: 3-14.

1. adatfeltárás: Outlier exploration

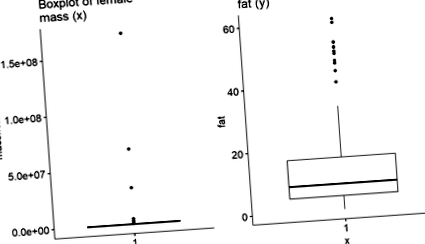
Adatfeltárás 1a: Külső feltárás boxplotokkal

Ebben az elemzésben a fő változók a következők

Prediktor (x): Az anyák testtömege (mass.fem)
Válasz (y): a tej (zsír)% tejzsír

Mindegyiket megnézem egy dobozban. Ha nem csoportosító változóval ábrázolok, akkor nincs szükségem x-re a ggboxplot ().

Minden egyes ábrát elkészítek és R objektumban tárolok, majd egymás mellé készítek egy diagramot a cowplot: plot_grid () használatával.

1. készítsd el a grafikonokat

Úgy tűnik, hogy az anyagtömegben kiemelkedők vannak. Meglátom, hogy a napló transzformáció segít-e ebben.

Táblázat (tömeg) és zsír

1b. Adatfeltárás: Outlier exploration dotplots

A (Cleveland) dotplot (vagy dotchart) több dologra is utalhat. Adatfeltárás és diagnosztika céljából a Cleveland dotplot számértéket (x vagy y) ábrázol egy indexértékhez képest. Az index értéke lehet

a megfigyelés sorrendje az adatokban (1 = 1. megfigyelés)
a megfigyelés rangja az adatokon belül (1 = legkisebb megfigyelés)

A ggpubr-ban a ggdotchart () függvény a változó számértéket veszi y változónak. Az x változóhoz a ggdotchart vehet numerikus vagy kategorikus változót. A ggdotchart () ezután az y-változót a legkisebbtől a legnagyobb értékig rendezi, és az x tengellyel szemben ábrázolja, amelyet kategorikus változóként kezelnek (még ha numerikus is). Ez némileg eltér attól, amit az alap R dotchart () függvény tesz, amelyet a Zuur és mtsai 2010 cikk tartalmaz.

Az x változóhoz szerintem jól működik, ha megadjuk a ggdotchart () -t is

Egy kategorikus változó, sok szinttel
Index nagyságrendű

Pontválasz az (y) válaszváltozó számára

Ábrázolja a pontdiagramot az index értéke alapján. A ggpubr lehetővé teszi számunkra, hogy a biom segítségével színezzük a kódot, ami nagyon jó. Összességében, amit keresünk, egy nagy ugrás az adatpontok között, ami egy szokatlan megfigyelést jelez, amelyet a adatbeviteli hiba.

Fogyókúránként is szemlélhetjük

Ábrázolja a pontdiagramot fajok alapján. Ez csúnya, mert a fajnevek olyan hosszúak.

Családonként több faj létezik; ez érdekes perspektívát kínál arra vonatkozóan, hogy a méret hogyan viszonyul a családhoz, mert az y tengely mentén több érték van az egyes tengelyek mentén az x tengely mentén.

Hasonló a családnál, kivéve a több pontot. Ne feledje, hogy a húsevő most kiemelkedik, mivel viszonylag nagy a variációja

Pontjel a prediktor változóhoz (x)

Húsevőimben vannak olyan adatpontok, amelyek sokat ragadnak. Ez aggályos lehet. Két dolog azonban

1. Van egy sima felpörgetés; vagyis a legmagasabb pont a növekvő trend része.
1. Tudom, hogy ezek az adatok az emlősök tömegét jelentik, amelyek egérenként változóak.

Tehát ez a dotplot nem vonatkozik, de mindenképp ellenőriznem kell a magas értékeket. Nem ártana az átalakítást naplózni és utána újra ellenőrizni.

2. adatfeltárás: Y homogenitása a Conditional boxplot segítségével

A feltételes boxplot az adatok doboza, az érintett csoportok szerint elosztva. Az adatok elosztása (a dobozdiagram) tehát a csoportosítási változótól függ vagy attól függ. Matyás kifejezéssel írhatunk „disztribúció (y | csoport)”, ahol „|” jelentése: attól függ. (ez nem valós dolog, csak feltételezhetően fel kell idéznie a valószínűség-állítást, mint például Pr (Ho | adatok)).

Az y változó homogenitása lineáris modellek feltételezése - és fontos. (Emlékezzünk vissza, hogy a „homogenitás” a variancia homogenitására, más néven homoskedaszticitásra utal.) Ezzel szemben a lineáris modellek nem feltételeznek semmit az x változó eloszlásáról. Jó ötlet, hogy az x (prediktor) változókból is készítsen dobozos ábrákat, csak azért, hogy megbizonyosodjon arról, hogy ismeri az adatokat, és hogy nincs semmi ostoba.

Ha a dolgok nem homogének (= heterszkasztikusak), az átalakulás segíthet a dolgok rendbetételében. A következőkben a boxplot segítségével feltárom az x és y változókat, és kipróbálok egy log transzformációt a dolgok kijavításához.

Transzformálatlan tejzsír adatok feltételes boxplot

Az adatok nem torzak, de:

Úgy tűnik, hogy a variancia csoportonként eltérő
A százalékos adatok szükségszerűen 0 és 100% között vannak korlátozva, így eredendően nem normálisak

Átalakított adatok feltételes boxplot

Az átalakulás stabilizálja a varianciát.

X változó feltárás: Női méretű feltételes boxplots

Nem feltételezzük, hogy az X változó homogén, de jó feltárni az adatokat feltételes boxplots segítségével is.

Transzformálatlan méretadatok

Az adatok erősen torzak, ami a magas tőkeáttétel miatt befolyásos adatpontokat hoz létre.

Átalakított méretadatok

3. adatfeltárás: Normalitás

„A lineáris regresszióban tulajdonképpen az összes ismételt megfigyelés normalitását feltételezzük egy adott kovária értéken ... A nyers adatok normalitása azonban a maradványok normalitását is magában foglalja” (Zuur et al 2010)

A normalitás feltételezésével általában a modell illesztése után lehet a legjobban foglalkozni. Azonban megkezdheti annak értelmét, ha az adatok hisztogramjait (és bizonyos mértékig boxplot-ját) megrajzolja főbb csoportosító változók („Zuur nomenklatúráját használó„ feltételes boxplots ”) alapján felosztva. Ez a kondicionálás a ggplot faceting képességének felhasználásával valósítható meg.

Ha t-tesztet vagy ANOVA-t végez, a csoportonként feltételesen feltételezett nyers adatok ezen hisztogramjai egyenértékűek lesznek a maradék diagramjaival a modell illesztése után. Az ANCOVA és a többszörös regresszió esetén azonban ténylegesen illeszkednie kell a modellhez.

Vegye figyelembe, hogy a normalitás az y változóra vonatkozik. Soha nem árt feltárni az x változót is.

Már tudom, hogy napló transzformációra van szükség, ezért kihagyom a nyers adatokat, és csak megnézem a log10 értékeket

Regressziót fogok végezni, ezért be kell illesztenem egy modellt. Vannak azonban fontosabb kategorikus változók, amelyeket figyelembe kell vennem, ezért elkészítek egy hisztogramot, hogy megnézzem, hogyan néz ki.

A naplótranszformáció után sem szuper normálisak az adatok. A biom további kondicionálása azonban ezt jobbá teheti; továbbá, amint már mondtam, igazából illeszkednem kell a regressziós modellemhez, és meg kell néznem a maradékokat, hogy valóban ítéletet mondjak. Ráadásul nem szoktam lógni a normálistól, hacsak a dolgok valóban nem torzak.

Indirekt módon hozzáadhatnám a biomot úgy, hogy létrehozok egy kombinált változót „híváscsoport”

Ebből kiderül, hogy a földi ragadozók kissé torzak. Kevés adatponttal azonban nehéz megmondani. Összességében ezek az adatok normálisak, de lásd a fenti figyelmeztetéseket, hogy miért nem a legkevésbé aggódom ebben a szakaszban.

Adatok feltárása Scatter-diagramokkal

A prediktorok és a válaszváltozók szóródási diagramja szintén kulcsfontosságú az adatok feltárásában, valamint a végső adatok bemutatásában

Szétszórt nyers adatok

Már tudom, hogy a napló transzformáció valószínűleg kulcsfontosságú ezen adatok kezeléséhez, de érdekes a nyers adatokat megnézni. Láthatjuk, hogy a szélsőjobboldali adatpont hogyan hat a regressziós vonalon.

A transzformált adatok szóródási ábrája

A log transzformáció magas tőkeáttételi értékekkel foglalkozik (az állatok nagy mérete miatt a szélsőséges x tengely értékek), behúzza a potenciális y tengelyen kívül eső értékeket, javítja a normalitást és stabilizálja a csoportokon belüli szórást. Fantasztikus!

Egy probléma továbbra is fennáll. Ez a szórásdiagram azt jelzi, hogy az egyes főcsoportok közötti szórás a méret növekedésével növekszik. Ez még a napló által transzformált adatokban is előfordul. Ez a fő kérdés, amelyet csak általánosított legkisebb négyzetek (GLS) és/vagy véletlenszerű effektusok segítségével lehet megoldani. További részletekért lásd a következő dokumentumot

Cleasby és Nakagawa. 2011. elhanyagolt biológiai minták a maradványokban. Viselkedésökológia és szociobiológia.

Más Scatter plot elemek

Adjon hozzá egy „szőnyeget” az adateloszlások megjelenítésének elősegítéséhez.

Adja hozzá az átlagos pontot és a szórási görbe ellipszist

Adjon hozzá egy pontot az adatok kétváltozós átlagához (együttes átlag mindkét tengely mentén). Vegye figyelembe, hogyan esik a regressziós vonalra.

Adjon hozzá egy „adatelipszist” is

"Az adatellipszist általában vizuális összefoglaló hozzáadásához használják egy szóródási sávhoz, feltüntetve a két változó regressziós vonalának átlagát, szórását, korrelációját és meredekségét." (Friendly et al 2013 Elliptical Insights: Statisztikai módszerek megértése elliptikus geometrián keresztül)

Az ellipszis mindkét dimenzióban 95% -os konfidencia intervallum. Kiszámíthatja az x változó átlagát, és kiszámíthat egy konfidencia intervallumot, majd kiszámíthatja az y változó átlagát és a 95% -os CI-t. Az ellipszis alapvetően egyszerre egyesíti ezt a két dolgot.

4. adatfeltárás: A felesleges nullák

Ha meg van számlálva az adatok, gyakran használja a Poisson regressziót. A lineáris regresszióhoz hasonlóan a Poisson-regresszió is feltételezéseket tesz az adatok eloszlására vonatkozóan. A sok nullával rendelkező számláló adatok sértik ezeket a feltételezéseket.

Adatok feltárása: kollinearitás

Amikor a prediktor változók szoros összefüggésben vannak egymással, ez problémát okoz a regresszió becslésében és következtetésében.

Elemzésem csak a női tömegre összpontosít, mint numerikus előrejelző. Az eredeti elemzés számos más előrejelzőt vett figyelembe, de nem tárgyalta kifejezetten a kollinearitás kérdéseit.

Összefüggések táblázata

A kollinearitás érzékelésének egyik módja a korrelációs együtthatók táblázatának megnézése az előrejelzők számára. Hozzáadom a válasz változó zsírtartalmát is.

A korrelációkhoz p-értéket kaphat a pszichológiai csomag corr.test segítségével

Ne feledje, hogy a változók tökéletesen korrelálnak egymással, így az átlós elemek mindegyike 1. A magas pozitív vagy negatív értékek erősen korrelált értékeket jeleznek, amelyek problémákat vetnek fel, ha mindkettő szerepel a regresszióban. A kollinearitás azonban finom lehet, ezért a variancia inflációs tényezőket alkalmazó teljes diagnosztikát kell használni, amint a modell illeszkedik.

Ennek vizuális megjelenítését a GGally: ggpairs segítségével kaphatjuk meg, amely a sactterplot mátrix, hisztogramok az egyes változókhoz, valamint a korrelációs koeffeictions.

GGally: ggpairs elég lassú; a régimódi párok () gyorsabbak.

Hozzáadhat összefüggéseket és hisztogramokat, ha hozzáad néhány funkciót. A részletekért lásd a súgófájl párokat.

A variancia-inflációs tényezőkről lásd: Graham 2003. A multicollinearity szembenézése az ökológiai többszörös regresszióban. Ökológia.

Az egyetértésről bővebben lásd: Freckleton. 2011. A kollinearitás kezelése a viselkedési és ökológiai adatokban: modellátlagolás és a mérési hiba problémái. Viselkedésökológia és szociobiológia. https://link.springer.com/article/10.1007/s00265-010-1045-6

6. adatfeltárás: Kapcsolat y & x között

Megnéztük már az x versus y változó és a szóródási sáv mátrixának szórási sávját.

Egy dolog, amit nem emeltek ki, az az, hogy a ggscatter () nem lineáris „simító” az add = „lösz” kifejezéssel. Ez hasznos lehet annak megállapításához, hogy vannak-e nemlineáris összefüggések.

7. adatfeltárás: Figyelembe kell-e vennünk az interakciókat?

Amikor kölcsönhatások lépnek fel, két változó kapcsolata függ egy harmadiktól. Például a színnel és/vagy a fent használt fazettával kódolt szóródási pontok azt jelzik, hogy a zsír meredeksége a testmérethez képest pozitív a vízi húsevőknél, de negatív más csoportoknál.

8. adatfeltárás: A válaszváltozó megfigyelései függetlenek-e?

Ha az adatokat idősor részeként gyűjtik, ismételt méréseket végeznek ugyanazon a dologon, vagy a tér szomszédos rögzített pontjaiból az autokorrelációs mintázatokra van lehetőség. Ez nem alkalmazható az emlősök tejadatkészletére.

Az adatoknak vannak problémái a filogenetikai felépítéssel. Ezt legjobban filogenetikai reression módszerekkel lehetne kezelni; Nincs kéznél a filogenitás, ezért ennek közelítésére a Rend, a Család és a Nemzetek durva szintű klaszterezését fogom használni.

Numerikus adat-összefoglalók

Nagyon hasznos lehet numerikus adat-összefoglalókat készíteni, amelyek segítenek Önnek és az olvasóknak megérteni az adatokat. Ezt Zuur nem hangsúlyozza