Veszteségfelületek, módkapcsolat és a DNN-ek gyors összeállítása Pavel s Blog

Blogpost Pavel Izmailov, Timur Garipov és Andrew Gordon Wilson; vizualizációk együttműködésben Javier Ideami.

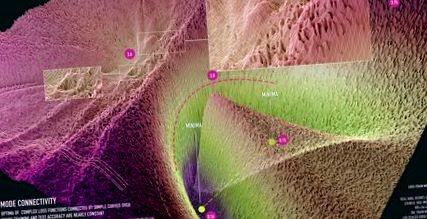
1.ábra: a ResNet-20 üzemmód-kapcsolatának megjelenítése a CIFAR-10 adatkészleten átugrás nélküli kapcsolatok nélkül. A megjelenítés Javier Ideami (https://losslandscape.com/) együttműködésével készült.

A mély neurális hálózatok általánosításának megértése nagy nyitott kérdés. Az ideghálózatokat úgy képzik ki, hogy minimalizálják a nagyon multimodális veszteségfelületeket, sok olyan paraméter-beállítással, amelyek nem eredményeznek edzésvesztést, de gyenge általánosítást. Ezen veszteségfelületek geometriai tulajdonságainak megértésével elkezdhetjük ezeket a kérdéseket megoldani és hatékonyabb edzési eljárásokat építeni. Valójában a veszteségfelületek helyi simaságát és konvexitását használják az SGD és más optimalizálók konvergenciájának elemzésére [pl. g. 12]. Nemrégiben sztochasztikus súlyátlagolást [5] javasoltak a veszteség laposabb régióinak megtalálásához, ami jobb általánosításhoz vezetett.

A felület alakja nagy hatással van a mély tanulás bayesi megközelítésére is. Bayesi megközelítéssel nem csak egyetlen pontot akarunk találni, amely optimalizálja a kockázatot, hanem inkább egy veszteségfelületen integrálódni, hogy Bayes-modell átlagot alkossunk. A veszteség felületének geometriai tulajdonságai, nem pedig az optima specifikus helyei, ezért nagyban befolyásolják a prediktív eloszlást egy Bayes-i eljárásban. Ennek megfelelően a legújabb megközelítések az SGD pályájának geometriáját használták fel skálázható és nagy teljesítményű bayesi következtetési eljárásokhoz [6, 7].

Ezeknek a veszteségfelületeknek a tulajdonságairól még mindig nagyon keveset tudunk. Új felfedezések történnek, amelyek topológiai viselkedést mutatnak, amely nagyon különbözik az idegi hálózatoktól. Ebben a blogbejegyzésben a módkapcsolatot írjuk le, amely a NeurIPS 2018 cikkünkben bemutatott modern neurális nettó veszteség tájak meglepő tulajdonsága. Ebben a bejegyzésben szereplő kifejtésünk az intuíció vizualizáció útján történő megszerzésére koncentrál.

Jellemzően a mély ideghálózatok lokális optimáját elszigetelt medencékként képzeljük el, mint a 2. ábra bal oldali paneljén. Ebben az ábrán három egymástól függetlenül képzett hálózat összes affin kombinációjából képzett síkban jelenítjük meg a nagy dimenziós veszteség felületét. A következő részben leírjuk a vizualizációs eljárás részleteit. Ez az intuíció a következő kísérletből származik: ha két azonos architektúrájú hálózatot képezünk, akkor két különböző lokális optimát kapunk a paramétertérben; a két megoldást összekötő vonalszakasz mentén bekövetkező veszteség felrobbant az optima között, elérve az inicializáláskor teljesen képzetlen hálózatok által elért értékeket. Meglepő módon az optimák valójában nem elszigeteltek. Görbe utat találhatunk közöttük, így a veszteség gyakorlatilag állandó az út mentén. Ezt a jelenséget módkapcsolatnak nevezzük. Ezek az ívelt utak nagyon egyszerűek lehetnek, például a 2. ábra középső és jobb oldali paneljén láthatók. Ezeket az utakat szintén könnyű megtalálni, ahogyan az alábbiakban elmagyarázzuk.

2. ábra: A ResNet-164 felületének vesztesége a CIFAR-100 készüléken. Bal: három optima a függetlenül képzett hálózatokhoz; Középső és Jobb: Négyzetes Bezier-görbe és egy sokszögű lánc egy kanyarral, amely összeköti a bal alsó panel két alsó optimáját egy majdnem állandó veszteség útján.

Bemutatták, hogy a módkapcsolat nagyon általános. [1, 2] módban több korszerű képbesorolási architektúra és a szöveges adatok néhány ismétlődő architektúrája esetén mutatható ki a kapcsolat. A [3] cikkben a szerzők azt mutatják, hogy lehetőség van különböző optimalizálókkal és hiperparaméterekkel képzett optimák összekapcsolására, mint például a kötegméretek, a súlycsökkenés, a tanulási sebesség ütemezése és az adatnövelési stratégia. [4] -ben a szerzők szerint a módkapcsolatosság érvényesül a szakpolitikai optimalizálási algoritmusok számára a mély megerősítéses tanulás során.

Hogyan lehet vizualizálni a veszteséges felületeket?

A vizualizáció segít elemezni és felépíteni a bonyolult objektumokkal kapcsolatos intuíciókat. A dimenziócsökkentésen alapuló vizualizációk értelmezhető struktúrát tárhatnak fel, ami új tudományos felismerésekhez vezethet; például [11] -ban a t-SNE vizualizációkat használták fel a retina sejtek új altípusainak felfedezésére. Itt tanulmányozzuk a mély ideghálózatok veszteségfüggvényeinek tulajdonságait, amelyek millióktól (vagy néha akár milliárdoktól) függenek. Nem tudunk közvetlenül vizualizálni egy millió dimenziós felületet. Megtekinthetjük azonban a veszteségfüggvény 2D-s szeletét, és ha ezt a szeletet gondosan választjuk meg, betekintést nyújthat a táj felépítésébe.

3. ábra: A veszteség felület vizualizációs eljárásának illusztrációja. Válasszunk egy 2D síkot az idegháló paraméterterében, felépítünk egy koordinátarendszert a síkban és meghatározunk egy rácsot ebben a koordinátarendszerben. Ezután kiértékeljük a rács egyes pontjainak veszteségét, és megjelenítjük az eredményt.

A paramétertér három pontja mindig egyedi 2D síkot határoz meg, amely áthalad ezeken a pontokon. Tegyük fel, hogy a súlytérben három pontunk van (w_1, w_2, w_3 \). Ezek lehetnek például három, egymástól függetlenül képzett hálózat paramétereinek vektorai (az összes tömeg és előfeszítés egyetlen vektorba összefűzve), mint a 2. ábra bal oldali paneljében. Felépíthetünk egy \ (w_1, w_2, w_3 \) az alábbiak szerint. Meghatározzuk a sík alapját \ (u = (w_2-w_1), v = (w_3-w_1) \) és az eltolásvektort \ (w_1 \) értékre. Ortogonalizálhatjuk az alapot úgy, hogy átállunk a \ (v = v - cos (u, v) u \) értékre, ahol \ (cos (u, v) \) a \ (u \) és \ vektorok közötti szög koszinusa. (v \). Ezután definiálhatunk derékszögű koordinátarendszert a síkban, és \ ((x, y) \) koordinátákat térképezhetünk fel az eredeti paramétertérben lévő pontokhoz a \ (w (x, y) = w_1 + u \ cdot x + képlet segítségével. v \ cdot y \). Most felépíthetünk egy rácsot a koordinátarendszerben, és kiértékelhetjük a hálózat veszteségfüggvényét, amely megfelel a rács egyes pontjainak, és megjeleníthetjük az eredményeket. A 3. ábra szemlélteti a megjelenítés folyamatát.

Útvonalak keresése a módok között

Az optimális párok közötti alacsony veszteségű út megtalálásának módja intuitív módon nagyon egyszerű: paraméterezzük az utat és minimalizáljuk az út mentén az átlagos veszteséget annak paramétereihez képest. Formálisan tegyük fel, hogy két veszteségfüggvényünk van \ (w_1 \) és \ (w_2 \). Ezután definiáljuk az őket összekötő utat \ (\ phi (t) \), egy leképezést a \ ([0, 1] \) szegmensből a paramétertérbe úgy, hogy \ (\ phi (0) = w_1, \ phi (1) = w_2 \). Például használhatunk másodfokú Bezier görbét: \ (\ phi (t) = (1 - t) ^ 2 w_1 + 2t (1-t) \ theta + t ^ 2 w_2 \), fekete vonallal ábrázolva A 2. ábra középső panelje. Itt látható a görbe paramétere, amelynek mérete és szerkezete megegyezik a \ (w_1 \) és \ (w_2 \) súlyvektorokkal. Azért edzünk, hogy minimalizáljuk a görbe átlagos veszteségét. Pontosabban minimalizáljuk

a \ (\ theta \) vonatkozásában, ahol \ (Loss () \) a hálózatok kiképzéséhez használt standard veszteségfüggvény \ (w_1 \), \ (w_2 \), például kereszt-entrópia veszteség a besoroláshoz.

Hatékonyan kiszámíthatjuk a \ (L (\ theta) \) sztochasztikus gradienseit a \ (\ theta \) vonatkozásában. Ehhez egyenletesen mintát veszünk egy \ (t \) pontról \ ([0, 1] \), majd kiszámoljuk a \ (Loss (\ phi (t)) \) gradiensét a \ (\ theta \) a láncszabály használatával:

Ennek a sztochasztikus gradiens becslésnek a felhasználásával minimalizáljuk a \ (L (\ theta) \) értékeket standard SGD-vel.

A másodfokú Bezier-görbe esetében a \ (\ phi (t) \) teljes út a paramétertér 2-dimenziós alterében található. A veszteségfüggvényt ezen a síkon jeleníthetjük meg az edzés során, az előző szakaszban leírt vizualizációs eljárás segítségével.

Az üzemmód-összeköttetés nagy felbontású vizualizációi

Javier Ideami-mal együttműködve a közelmúltban nagy felbontású vizualizációkat készítettünk a módkapcsolatot tartalmazó síkok veszteségfelületeiről. Készítettünk egy videót, amely egy kvadratikus Bezier-görbe képzési folyamatát mutatja, amely összekapcsol egy pár helyi optimát a ResNet-20-hoz, a CIFAR-10-nél nincsenek kihagyási kapcsolatok:

A videóban az optimák a véletlenszerűen inicializált görbe elkülönítésétől és leválasztásától kezdve alacsony veszteségű alagúttal vannak összekötve, az 1. ábra szerint.

A FastAI Imagenette adatkészleten még nagyobb, 1000x1000 felbontással hoztuk létre a ResNet-20 statikus megjelenítését. Ezeket a vizualizációkat a 4., 5., 6. ábrán mutatjuk be.

4. ábra: A ResNet-20 üzemmód-kapcsolatának megjelenítése az átmenet nélküli kapcsolatok nélkül az ImageNet adatkészleten. A megjelenítés Javier Ideami (https://losslandscape.com/) együttműködésével jött létre.

5. ábra: a ResNet-20 üzemmód-kapcsolatának megjelenítése az átugrás nélküli kapcsolatok nélkül az Imagenette adatkészleten. A megjelenítés Javier Ideami (https://losslandscape.com/) együttműködésével jött létre.

6. ábra: a ResNet-20 üzemmód-kapcsolatának megjelenítése az átugrás nélküli kapcsolatok nélkül az Imagenette adatkészleten. A megjelenítés Javier Ideami (https://losslandscape.com/) együttműködésével jött létre.

Javier webhelyén, a https://losslandscape.com/ oldalon találhat más, művészi, nagy felbontású vizualizációkat a neurális hálózatvesztési felületekről, statikus és dinamikus formában egyaránt.

A vizualizációk létrehozásának számítási költségei

Az egyes vizualizációkhoz kiszámoljuk a rács minden pontjának veszteségét (amely megfelel a hálózati súlyok eltérő beállításának). A 4., 5., 6. ábrákhoz 1000x1000 rácsot használtunk, amely megköveteli egy neurális hálózat veszteségének értékelését a paraméterek millió különböző beállításánál. A videóhoz 600 keretet számoltunk 300x300 felbontással, ami több mint 50 millió veszteségértékelést jelent. A számítási költségek korlátozása érdekében az adatkészlet egy mintavételezett változatát használjuk, ügyelve arra, hogy ez az alminta megőrizze a struktúrát a vizualizációkban. Még a kisebb adatállomány mellett is, a videó megjelenítési folyamata két hétig tartott, 15 GPU használatával. A 4., 5., 6. ábrán látható nagyfelbontású statikus vizualizációk létrehozása körülbelül két napig tartott három GPU használatával.

Különböző ábrázolásokat tartalmaznak-e ezek az utak?

A neurális hálózatok paraméterezése köztudottan degenerációkat tartalmaz. Például a ReLU hálózatokban meg lehet szorozni egy rétegben lévő súlyokat egy bizonyos értékkel, és a következő réteg súlyait el lehet osztani ugyanezzel az értékkel, és a hálózat kimenete (és ennek következtében veszteség) nem változna. Természetes tehát megkérdezni, hogy a módkapcsolat csak a paraméterezés ilyen degenerációi miatt létezik-e. Ehelyett azt tapasztaljuk, hogy az alacsony veszteségű utak a különféle ábrázolások gazdag gyűjteményét tartalmazzák, amelyek különböző előrejelzéseket nyújtanak a tesztadatokra vonatkozóan. Az 1D regressziós probléma alacsony veszteséges útján mutatott funkciók sokféleségét a 7. ábrán mutatjuk be.

7. ábra: Veszteségfelület a 2D síkban, amely alacsony veszteségű utat (jobbra) és a prediktív funkciókat tartalmaz, amelyek ennek a síknak (balra) különböző pontjainak felelnek meg az 1D regressziós problémára edzett DNN számára. A jobb oldali bíbor színű körökkel ábrázolt görbe különböző pontjai megfelelnek a bal oldali bíborvonallal ábrázolt különböző funkcióknak. A kísérlet részletes leírását a [7] oldalon találja.

A görbék valóban összekapcsolnak egy pár különböző optima \ (w_1 \) és \ (w_2 \) párhuzamot, amelyek különböző előrejelzéseket hoznak létre. Ezért az előrejelzéseknek valamilyen módon meg kell változniuk a görbe mentén. Megállapíthatjuk, hogy a \ (\ phi \) út mentén a hálózatok előrejelzései jelentősen eltérnek-e, ha megvizsgáljuk e hálózatok együtteseinek teljesítményét. Két hálózat együtteseit vesszük figyelembe: az egyik fix értéke \ (w_1 \), a másik \ (\ phi (t) \) a \ (w_2 \) felé halad a \ (\ phi \) útvonal mentén. Megállapítottuk, hogy a \ (w_1 \) és a \ (\ phi (t) \) együttes ugyanúgy teljesít, mint a függetlenül képzett \ (w_1 \) és \ (w_2 \) együttese még \ (t \ kb 0,3 \ esetén is) ), ami azt sugallja, hogy az útvonal mentén lévő hálózatok értelmesen különböznek a végpontoktól. Az együttes teljesítményét a görbe pontjának függvényében vizualizáljuk a 8. ábrán.

8. ábra: Az útvonal végpontjának és az útvonal egy pontjának együttese az útvonal pontjának függvényében. Összehasonlításképpen az együttes teljesítményt vizualizáljuk az optimát összekötő közvetlen vonalas szakaszra, valamint a módszerünkkel megtanult útra.

Új Munka

Számos tanulmány elméleti magyarázatot ad a mód-kapcsolatokról. Például a közelmúltbeli tanulmány [4] bemutatja, hogy a zajstabilitás különböző elképzelései, például a stabilitás a lemorzsolódási zavarokig, üzemmód-összeköttetést jelentenek. A tanulmányok [8, 9] különböző elméleti perspektívákat nyújtanak az üzemmód-összekapcsolhatóságról, megmutatva, hogy bizonyos feltételezések mellett a DNN veszteség összes alszint halmaza összekapcsolódik.

A módkapcsolat új gyakorlati módszereket inspirált az ideghálózatok képzésére, javított általánosítással és bizonytalansági számszerűsítéssel. Magas szinten a módkapcsolat azt mutatja, hogy a veszteségfüggvény különböző módjai között lehet utazni anélkül, hogy általános kis veszteségtartományt hagynánk. A sztochasztikus súlyátlagolás (SWA) [5] ezt az ötletet használja, és különféle megoldásokat tár fel az adott megoldás körül azáltal, hogy az SGD-t magas, állandó tanulási sebességgel futtatja; majd a különböző korszakokból származó SGD-iterációkat átlagolva új megoldást kapunk, jelentősen javított általánosítással. Az SWA-Gaussian [6] kiterjeszti az SWA-t, hogy az SGD kovarianciáját is megismételje és Gauss-eloszlást konstruáljon a súlyokon; Ha ebből az eloszlásból mintát veszünk egy Bayes-modell átlagának létrehozására, jelentősen javítható mind a modell pontossága, mind a bizonytalansági ábrázolás a standard SGD-hez képest. Végül [7] megközelíti a Bayes-féle hátsó részt az optima közötti alacsony veszteségű utat tartalmazó altér hálózatának súlya felett, és ezen közelítés segítségével átlagolja a Bayes-modellt.

A közelmúltbeli tanulmány [10] kiterjeszti módszerünket az alacsony veszteséggörbék megtalálásához, hogy olyan síkokat találjon, ahol a veszteségfelület hasonlít egy adott képhez. Meglepő módon minden olyan képhez képesek voltak ilyen síkokat találni. Néhány veszteségfelületüket bemutatjuk a 9. ábrán. Az a tény, hogy az egyszerű SGD könnyen megtalálja ezeket a bonyolult szerkezeteket a veszteségfelületben, a dimenzió megáldására utal. A paramétertér nagy dimenzionalitása sok utat kínál a jó megoldások felé.

9. ábra: a veszteség vizualizálása a [10] -ben felépített síkokban a FashionMNIST és a CIFAR-10 adatkészletekhez. Ezt az ábrát közvetlenül a [10] helyről másolják.

Hivatkozások

[1] Veszteségfelületek, módkapcsolat és a DNN-ek gyors összeállítása; Timur Garipov, Pavel Izmailov, Dmitry Podoprikhin, Dmitry Vetrov, Andrew Gordon Wilson; Neural Information Processing Systems (NeurIPS), 2018

[2] Alapvetően nincsenek akadályok az ideghálózat energiaellátásában; Felix Draxler, Kambis Veschgini, Manfred Salmhofer, Fred A. Hamprecht; Nemzetközi Gépi Konferencia (ICML), 2018.

[3] A mély tanulási heurisztika közelebbi pillantása: a tanulási arány újraindul, felmelegedés és lepárlás; A. Gotmare, N. Keskar, C. Xiong és R. Socher; Nemzetközi konferencia a tanulási képviseletekről (ICLR) 2019

[4] Az entrópia politikai optimalizálásra gyakorolt hatásának megértése; Zafarali Ahmed, Nicolas Le Roux, Mohammad Norouzi, Dale Schuurmans; Nemzetközi konferencia a tanulási képviseletekről (ICLR) 2019

[4] Olcsó megoldások tájképi összekapcsolhatóságának magyarázata többrétegű hálózatokhoz; Rohith Kuditipudi, Xiang Wang, Holden Lee, Yi Zhang, Zhiyuan Li, Wei Hu, Rong Ge, Sanjeev Arora; Neurális információfeldolgozó rendszerek (NeurIPS), 2019

[5] A súlyok átlagolása szélesebb optimához és jobb általánosításhoz vezet; Pavel Izmailov, Dmitrij Podoprikhin, Timur Garipov, Dmitry Vetrov, Andrew Gordon Wilson; Bizonytalanság a mesterséges intelligenciában (UAI), 2018

[6] Egyszerű alapállás a Bayes-i bizonytalansághoz a mély tanulásban Wesley Maddox, Timur Garipov, Pavel Izmailov, Dmitry Vetrov, Andrew Gordon Wilson Neural Information Processing Systems (NeurIPS), 2019

[7] Altér következtetés a Bayes-i mély tanuláshoz; Pavel Izmailov, Wesley J. Maddox, Polina Kirichenko, Timur Garipov, Dmitry Vetrov, Andrew Gordon Wilson; Bizonytalanság a mesterséges intelligenciában (UAI), 2019

[8] Az összekapcsolt alszintű halmazokról a mély tanulásban; Quynh Nguyen; Nemzetközi Gépi Konferencia (ICML), 2018.

[9] A félig rektifikált hálózatoptimalizálás topológiája és geometriája; C. Daniel Freeman, Joan Bruna

[10] Tájképi városnézés többpontos optimalizálással; Ivan Skorokhodov, Mihail Burtsev, 2019

[11] Nagymértékben párhuzamos genomszintű expressziós profilok készítése az egyes sejtekből nanoliteres cseppek segítségével