A teljes harmonikus torzítás (THD) megértése, kiszámítása és mérése

A teljes harmonikus torzítás (THD) egy olyan mérés, amely megmondja, hogy egy feszültség vagy áram torzításának mekkora része a jel harmonikusainak köszönhető.

A teljes harmonikus torzítás (THD) egy olyan mérés, amely megmondja, hogy egy feszültség vagy áram torzításának mekkora része a jel harmonikusainak köszönhető. A THD fontos szempont az audio, a kommunikációs és az energiaellátó rendszerekben, és általában, de nem mindig, a lehető legkisebbnek kell lennie.

Periódusos feszültség vagy áram harmonikus frekvenciái

A periodikus feszültség vagy áram harmonikus vagy harmonikus frekvenciái a jel frekvenciakomponensei, amelyek a főjel frekvenciájának egész sokszorosában vannak. Ez az az alapvető eredmény, amelyet a periodikus jel Fourier-elemzése mutat. A harmonikus torzítás a jel ezen harmonikusok által okozott torzulása.

A tisztán szinuszos feszültségnek vagy áramnak nincs harmonikus torzulása, mert ez egyetlen frekvenciából álló jel. A periodikus, de nem pusztán szinuszos feszültség vagy áram magasabb frekvenciájú komponenseket tartalmaz, amelyek hozzájárulnak a jel harmonikus torzulásához. Általánosságban elmondható, hogy minél kevesebb egy periodikus jel szinusz hullámnak tűnik, annál erősebbek a harmonikus komponensek és annál nagyobb lesz a harmonikus torzítás.

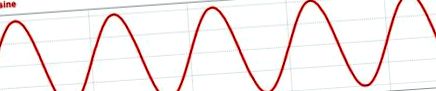
Tehát a tisztán szinuszos jelnek nincs torzulása, míg a négyzet alakú hullámnak, amely periodikus, de egyáltalán nem tűnik szinuszosnak, sok harmonikus torzítás lesz. A való világban természetesen a szinuszos feszültségek és áramok nem tökéletesen szinuszosak; bizonyos mértékű harmonikus torzulás jelen lesz. Az 1. és 2. ábra vizuálisan összehasonlítja a szinuszos feszültséget és a négyzethullámú feszültséget az időtartományban és a frekvenciatartományban.

1. ábra: Szinuszos feszültség és négyzethullámú feszültség az időtartományban.

2. ábra: Szinuszos feszültség és négyzethullámú feszültség a frekvenciatartományban; csak a négyzethullámnak van csúcsa a harmonikus frekvenciákon.

Könnyen belátható a harmonikus torzítás a négyzethullám időtartományának és frekvenciatartományának reprezentációjának vizsgálatakor, de fontos a harmonikus torzítás számszerűsítése is. A következő szakasz bemutatja, hogyan lehet ezt megtenni a metrikával Teljes harmonikus torzítás.

A teljes harmonikus torzítás kiszámítása

A THD az összes harmonikus frekvencia (RMS) ekvivalens gyökértékének (RMS) aránya (a 2. harmonikától kezdve) az alapfrekvencia RMS feszültségéhez viszonyítva (az alapfrekvencia a jel fő frekvenciája, azaz a frekvencia, amelyet azonosítana, ha a jelet oszcilloszkóppal vizsgálná). Az 1. egyenlet a THD matematikai definícióját mutatja (vegye figyelembe, hogy ebben az egyenletben feszültséget használnak, de helyette áramot lehet használni):

$$ V _ $$ az n-edik harmonikus RMS-feszültsége
$$ V _ $$ az alapfrekvencia RMS feszültsége

Mivel a harmonikusok amplitúdóira van szükség a THD kiszámításához, a THD meghatározásához Fourier-elemzés használható. A Fourier-elemzés ezen alkalmazásának megtekintéséhez nézzük meg az 50% -os munkaciklus négyzethullám egyszerű példáját. Az 50% -os munkaciklus négyzethullám Fourier-sorozatának ábrázolása a következő:

Bővített formában ez:

A kibővített forma azért hasznos, mert megnézi az egyes frekvenciakomponensek csúcsfeszültségét (Vpk), és a THD kiszámítható az egyes frekvenciakomponensek RMS-értékének (azaz $$ \ frac >> $$) meghatározásával, és mindet az 1. egyenlethez csatlakoztatva:

Ez az egyenlet nehézkessé válik, de egy dolgot észre kell venni, hogy a kifejezés minden tagjának van egy $$ \ frac \ pi> $$ komponense. Ezt az összetevőt ki lehet küszöbölni, és mivel mind a számlálóban, mind a nevezőben megjelenik, valójában törlődik, ami a négyzethullám THD kifejezését az alábbiak szerint hagyja:

A THD kiszámításához ebből a kifejezésből trükkös matematika szükséges. Ha az 5. egyenlet négyzetgyök alatti összegzése n = 1-nél kezdődik, akkor ez egy konvergens sorozat lesz, amely összeadja a $$ \ frac $$ értéket:

Az egyetlen különbség a 6. egyenletben szereplő kifejezés és az 5. egyenlet THD kiszámításakor a $$ \ left (\ sum _ ^ \ frac \ right) $$ között a $$ \ frac $$ értéke, amikor n értéke 1. Mivel ez az érték 1, a THD kifejezés összegzése újraírható a következőképpen:

Végül, ha ezt az egyenletet visszacsatlakoztatjuk a négyzethullám THD-egyenletéhez (5. egyenlet), a következőket kapjuk:

A kezdeti feltételezésünk, miszerint a négyzethullám sok harmonikus torzítással rendelkezik, a négyzethullám időbeli és frekvenciatartománybeli vizuális vizsgálatán alapult. A most elvégzett számítások megerősítik feltételezésünket. Egy négyzethullámnak valójában 48,3% a teljes harmonikus torzulása, vagyis a harmonikus RMS értéke az alapfrekvencia RMS körülbelül 48,3% -a.

A teljes harmonikus torzítás mérése

Az elméleti THD kiszámítása jó gyakorlat lehet, de sok munka lehet, és a gyakorlatban amúgy sem fogsz ideális jelet (pl. Tökéletes négyzethullámot) kapni. Ezeknek a számításoknak az eredménye tehát csak közelítést adhat a THD-hez, amelyet egy adott jeltípushoz kaphat. A gyakorlatban a THD-t meg kell mérni az alapfrekvencia és az összes harmonikus RMS-értékének megszerzéséhez. Ez a mérés többféleképpen is elvégezhető.

Az első módszer szerint szűrőkkel lehet a jelet két részre osztani: egy jelet, amelynek összes harmonikusa kiszűrt, csak az alapfrekvencia marad, és egy olyan jel, amelynek az alapfrekvenciája leszűrt, az összes harmonikus elhagyásával. Ezután meg lehet mérni a két rész RMS-értékét, és kiszámítható a THD:

Ennek a módszernek az a feje, hogy könnyű elvégezni ezeket a méréseket. Hátránya, hogy a zaj is beleszámít a mérésbe, így valóban megkapja a THD és a zaj mérését (bár az audiorendszerekben a THD + zaj is fontos mérés).

A THD mérésének második módszere az alapfrekvencia és az egyes harmonikusok amplitúdójának mérése, majd ezek felhasználásával a THD kiszámítása az 1. egyenlet segítségével. Ez a mérés könnyen elvégezhető egy spektrum analizátor vagy egy THD analizátor segítségével, amely automatikusan végrehajtja az 1. egyenletet . Alternatív mérési technika a feszültség- vagy áramadatok rögzítése, majd a gyűjtött adatokon Fourier-transzformáció végrehajtása. Az alábbi példa felvázolja a második módszer alkalmazását.

Példa THD mérésre

A 3. ábra blokkdiagramjának példája egy 1 kHz-es szinuszhullámot mutat át egy erősítőn, és létrehoz egy új, 1 kHz-es szinuszhullámot, amely némi keresztirányú torzulást mutat. Ezt az új hullámot egy spektrum analizátorba vezetik be, amely grafikusan megjeleníti számos harmonikus amplitúdóját.

3. ábra: Egy rendszer, amely keresztbe torzítást vezet be egy jelbe.

Nagyítva a torz szinusz hullám kimenetének frekvenciaspektrumát, láthatjuk az amplitúdókat számos harmonikus frekvencián:

4. ábra: Szinuszos feszültség frekvenciaspektruma keresztirányú torzítással.

Ebből a frekvenciaspektrumból kézzel mértem meg az egyes harmonikus frekvenciák amplitúdóját, és rögzítettem az adatokat az alábbi táblázatban:

A torz szinuszhullám harmonikusainak amplitúdója

Harmonikus	Amplitúdó
1	3,08V
3	0,308V
5.	0,159V
7	0,090V
9.	0,0487V
11.	0,0253V
13.	0,0164 V
15	0,010V

A páros és a 15. feletti harmonikusok amplitúdója közel 0, ezért nem vettem bele a számításomba.

A mért amplitúdók bekapcsolódnak a THD egyenletbe:

(ne feledje, hogy a feszültség amplitúdóit RMS feszültség helyett használhatom, mert a $$ V_ = \ frac $$, és mivel a $$ \ sqrt $$ minden esetben előfordul, ki lehet küszöbölni és törölni lehet).

Ezzel a számítással a THD értéke 0,118 vagy 11,8%.

Természetesen a THD analizátor automatizálja a THD kiszámításának folyamatát a harmonikus amplitúdóiból. THD analizátor használata ehhez a jelhez 11,9% -os értéket ad, ami megerősíti a manuális módszer pontosságát, amelyet most átéltem.

A THD jelentősége a rendszerekben

Ez a cikk áttekintést adott a THD-ről és annak meghatározásáról elméletileg és valós (szimulált) rendszerben is. De nem tárgyalta azokat a rendszereket, ahol a THD fontos mérés.

A THD többféle rendszerben fontos, beleértve az energiaellátó rendszereket is, ahol az alacsony THD magasabb teljesítménytényezőt, alacsonyabb csúcsáramokat és nagyobb hatékonyságot jelent; audio rendszerek, ahol az alacsony THD azt jelenti, hogy az audio jel az eredeti felvétel hűbb reprodukciója; és kommunikációs rendszerek, ahol az alacsony THD kevesebb interferenciát jelent más eszközökkel és nagyobb átviteli teljesítményt jelent az érdekelt jel számára.

Keressen olyan jövőbeni cikkeket, ahol részletesebben foglalkozom az ilyen típusú rendszerekkel.