Mély tanulás - gépi tanulás felhasználása a biológiai látás tanulmányozásához

Najib J. Majaj

Idegtudományi Központ, New York University, New York, NY, USA

Denis G. Pelli

Pszichológiai Tanszék és Idegtudományi Központ, New York University, New York, NY, USA

Absztrakt

Számos látástudományi tanulmány gépi tanulást alkalmaz, különösen a „mély tanulás” nevű verziót. Az idegtudósok a gépi tanulást használják az idegi válaszok dekódolására. Az észlelés tudósai megpróbálják megérteni, hogy az élő szervezetek hogyan ismerik fel a tárgyakat. Számukra a mély neurális hálózatok referencia pontosságot kínálnak a tanult ingerek felismeréséhez. Eredetileg a gépi tanulást az agy inspirálta. Ma a gépi tanulást statisztikai eszközként használják az agytevékenység dekódolására. Holnap a mély ideghálózatok válhatnak az agy működésének legjobb modelljévé. A gépi tanulás biológiai látásban való használatának ez a rövid áttekintése érinti annak erősségeit, gyengeségeit, mérföldköveit, vitáit és jelenlegi irányait. Reméljük, hogy itt segítünk a látástudósoknak felmérni, hogy a gépi tanulásnak milyen szerepet kell játszania kutatásában.

Bevezetés

Mit kínál a gépi tanulás a biológiai látástudósoknak? Az automatizált osztályozás eszközeként fejlesztették ki, a pontosságra optimalizálva. A gépi tanulást széles körben alkalmazzák (Brynjolfsson, 2018), a tőzsdei előrejelzés regressziójától kezdve a sakkozás megerősítő tanulásáig, itt azonban a besorolásra koncentrálunk. A fiziológusok az idegi aktivitás alapján azonosítják az ingereket. Az észlelés tanulmányozásához a fiziológusok mérik az idegi aktivitást, a pszichofizikusok pedig a nyílt válaszokat, például egy gombnyomást. A fiziológusok és a pszichofizikusok kezdik a mély tanulást az emberi és nem emberi főemlősök tárgyfelismerésének modelljeként tekinteni (Cadieu et al., 2014; Khaligh-Razavi & Kriegeskorte, 2014; Yamins et al., 2014; Ziskind, Hénaff, LeCun, & Pelli, 2014; Testolin, Stoianov és Zorzi, 2017). Feltételezzük, hogy olvasóink többsége hallott már a gépi tanulásról, de kíváncsi arra, hogy hasznos lenne-e saját kutatásában. Először néhány pluszának és mínuszának ismertetésével kezdjük.

Pluszok: Mire jó

Legalábbis a gépi tanulás hatékony eszköz a biológiai adatok értelmezéséhez. A gépi tanulás egy sajátos formája, a mély tanulás nagyon népszerű (1. ábra). Csak divat? A számítógépes látás esetében a régi paradigma a következő volt: a funkció észlelése, majd a szegmentálás, majd a csoportosítás (Marr, 1982). A gépi tanulási eszközökkel az új paradigma a feladat definiálása és a címkézett példák halmazának megadása, és az algoritmus felépíti az osztályozót. (Ez „felügyelt” tanulás; az alábbiakban a felügyelet nélküli tanulást tárgyaljuk.)

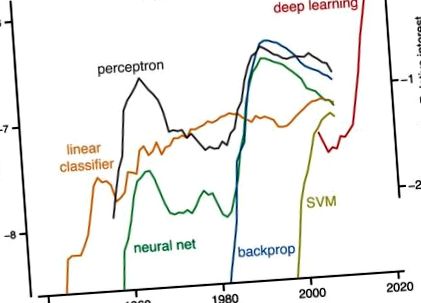
A népszerűség története. Baloldali skála: Az öt kifejezés - lineáris osztályozó, perceptron, támogató vektorgép, idegháló és háttámla (és nem mély tanulás) - megjelenési gyakorisága a Google által a megjelenés minden egyes évében indexelt könyvekben. A Google megszámolja n szó szavainak és kifejezéseinek előfordulását, és mindegyiket „ngrammak” nevezi. A gyakoriság az ilyen hosszúságú ngrammok összes példányának töredéke, az adott évben megjelent könyvek számával normalizálva (ngram/év/megjelent könyvek). Az ábrát a Google ngram nézőjével (https://books.google.com/ngrams) készítettük, amely az 1500 és 2008 között nyomtatott forrásokban található ngrammok éves számát tartalmazza. Jobboldali skála: A mély tanuláshoz a számok képviselik a keresési világszerte az adott év diagramjának legmagasabb pontjához viszonyítva a „mély tanulás” kifejezéshez (amint arról a https://trends.google.com/trends/ beszámolt). A jobboldali skála függőlegesen eltolódott, hogy 2004-ben megegyezzen a megfelelő (nem látható) mély tanulási ngram frekvenciával (bal oldali skála).

Háttámla: A „visszafelé terjedő hibák” rövidítése, széles körben használják a gradiens-ereszkedéses tanulás alkalmazására többrétegű hálózatokon. A számítási láncszabályt használja az egyes rétegek költségfüggvényének gradiensének iteratív kiszámításához.

Domborúság: A valós értékű függvényt akkor hívjuk „konvexnek”, ha a függvény grafikonjának bármely két pontja közötti vonalszakasz a grafikonon vagy felett helyezkedik el (Boyd & Vandenberghe, 2004). A probléma konvex, ha költségfüggvénye domború. A konvexitás garantálja, hogy a gradiens süllyedés mindig megtalálja a globális minimumot.

Konvolúciós ideghálózat (ConvNet): A Neocognitronban (Fukushima, 1980) gyökerező, a Hubel és Wiesel (1962) által leírt egyszerű és összetett sejtek ihlette ConvNets konvolúción és poolingon alapuló többrétegű neurális hálózatokon alkalmazza a backprop tanulást (LeCun et al., 1989; LeCun, Bottou, Bengio és Haffner, 1998).

Költségfüggvény: Olyan függvény, amely a megoldást és a kívánt kimenet közötti különbség mérésével valós számot rendel a megoldást jelölt költséghez. Az optimalizálással történő megoldás a költségek minimalizálását jelenti.

Keresztellenőrzés: Értékeli a hálózat általánosítási képességét az általa betanított adatokból az új adatokba.

Mély tanulás: A gépi tanulás sikeres és népszerű változata, amely több rejtett réteggel rendelkező back neurális hálózatokat használ. Az AlexNet, akkor az objektumfelismerés legjobb gépi tanulási hálózatának 2012-es sikere a fordulópont volt. A mély tanulás ma már mindenütt jelen van az interneten. Az elképzelés az, hogy a feldolgozás minden rétege egymás után bonyolultabb számításokat hajtson végre az adatokon annak érdekében, hogy a teljes többrétegű hálózat nagyobb kifejezőerőt kapjon. Hátránya, hogy a többrétegű hálózatok képzése sokkal nehezebb (Goodfellow et al., 2016).

Általánosítás: Mennyire teljesít jól egy osztályozó olyan új, nem látott példákon, amelyeket nem látott a képzés során.

Színátmenet: Olyan algoritmus, amely minimalizálja a költségeket azáltal, hogy a paramétereket fokozatosan megváltoztatja a költségfüggvény legmeredekebb ereszkedése irányába.

Hebbi tanulás: Hebb szabálya szerint a szinapszis hatékonysága növekszik a korrelált pre- és poszt-szinaptikus aktivitás után. Más szavakkal, az idegsejtek, amelyek együtt tüzelnek, összekapcsolódnak (Lowel & Singer, 1992). Tüske-időzítéstől függő plaszticitás néven is ismert (Caporale és Dan, 2008).

Gépi tanulás: Bármely számítógépes algoritmus, amely megtanulja a feladatok végrehajtását közvetlenül példákból, anélkül, hogy az ember kifejezett utasításokat vagy szabályokat adna meg ennek végrehajtására. A gépi tanulás egyik típusában, amelyet „felügyelt tanulásnak” neveznek, helyesen felcímkézett példákat kapunk a tanulási algoritmushoz, amelyet aztán „kiképeznek” (azaz paramétereit beállítják) a feladat önálló végrehajtására és láthatatlan példákra általánosításra.

Ideghálók: A biológiai ideghálózatok által inspirált számítógépes rendszerek, amelyek abból állnak, hogy az egyes idegsejtek megtanulják kapcsolataikat más idegsejtekkel, hogy példák figyelembevételével oldhassák meg a feladatokat.

Felügyelt tanulás: Bármely algoritmus, amely elfogadja a címkézett ingerek halmazát - egy edzéskészletet -, és visszaad egy osztályozót, amely fel tudja jelölni az edzéskészlethez hasonló ingereket.

Támogató vektor gép (SVM): A gépi tanulási algoritmus típusa az osztályozáshoz. Az SVM a „kernel trükk” segítségével gyorsan megtanulja a nemlineáris osztályozás elvégzését, ha többdimenziós térben talál egy olyan határt, amely elválasztja a különböző osztályokat, és maximalizálja az osztálypéldák és a határ közötti távolságot (Cortes & Vapnik, 1995).

Felügyelet nélküli tanulás: Felfedezi a struktúrát és a redundanciát a címkék nélküli adatokban. A számítógépes tudósok kevésbé használják, mint a felügyelt tanulást, de nagyon érdekes, mert a címkézett adatok szűkösek, míg a címkézetlen adatok bőségesek.

A 70-es és 80-as években népszerű kézimunka-felismeréssel (beleértve a szegmentálást és a csoportosítást) ellentétben a mély tanulási algoritmusok általánosak, csekély tartományspecifikusak. 1 A kézi tervezésű funkciódetektorokat az adatokból megismerhető szűrőkkel helyettesítik. A 90-es évek közepén elért haladás a gépi tanulásban hasznossá tette a gyakorlati osztályozáshoz, például a kézírás-felismeréshez (LeCun et al., 1989; Vapnik, 2013).

A gépi tanulás lehetővé teszi egy neurofiziológus számára az idegi aktivitás dekódolását a befogadó mezők ismerete nélkül (Seung & Sompolinsky, 1993; Hung. Kreiman, Poggio és DiCarlo, 2005). A gépi tanulás nagy lépés abban, hogy az idegtudományban a hangsúly áthelyeződik abból a szempontból, ahogy a sejtek kódolnak, és amit kódolnak - vagyis, hogy ez a kód mit mond nekünk az ingerről (Barlow, 1953; Geisler, 1989). A befogadó mező feltérképezése az idegtudomány alapja (kezdve Weber 1834. évi tapintható „szenzoros körök” feltérképezésével). Ehhez egyszer egysejtű felvételre volt szükség, percek vagy órák után kutatva, hogy egy sejt hogyan reagál mind a száz különböző ingerre. Ma egyértelmű, hogy egyetlen idegsejt befogadó mezőjének jellemzése, amely felbecsülhetetlen volt a retinában és a V1-ben, nem jellemzi, hogy a magasabb látóterek hogyan kódolják az ingert. A gépi tanulási technikák feltárják, hogy „hogyan lehet a neuronreakciókat a legjobban felhasználni (kombinálni) az észlelési döntéshozatal tájékoztatására” (Graf, Kohn, Jazayeri és Movshon, 2011). A gépi dekódolás egyszerűsége erény lehet, mivel lehetővé teszi számunkra, hogy felfedezzük, mi könnyen olvasható (például egyetlen downstream neuron által; Hung et al. 2005). A pszichofizikai teljesítményszintek elérése az ingerobjektum azonosságának és helyének dekódolásakor az idegi válaszból azt mutatja, hogy a mért idegi teljesítmény rendelkezik minden információval, amely a megfigyelő számára a feladat elvégzéséhez szükséges (Majaj, Hong, Solomon és DiCarlo, 2015; Hong, Yamins, Majaj és DiCarlo, 2016).

A mély tanulás viszont egy nagyon jó megfigyelõ, aki tanul, amely hasznos információkat szolgáltathat az emberi tanulásról. 2 Különösen felfedheti a tanulás korlátait, amelyeket az edzés során használt ingerek összessége szab. Továbbá, az SDT-vel ellentétben a mély neurális hálózatok megbirkóznak a valós feladatok bonyolultságával. Nehéz megmondani, hogy a viselkedési teljesítményt korlátozza-e az ingerek összessége, idegi reprezentációjuk vagy a megfigyelő döntési folyamata (Majaj et al., 2015). A besorolási teljesítményre gyakorolt hatás nem nyilvánvaló az ingercsaládok és idegi válaszaik közvetlen vizsgálatából. Az SDT meghatározza az optimális teljesítményt az ismert jelek osztályozásához, de nem mondja el, hogyan lehet általánosítani egy edzéskészleten túl. A gépi tanulás igen.

Mínuszok: Gyakori panaszok

Egyes biológusok rámutatnak, hogy az ideghálók nem egyeznek azzal, amit tudunk az idegsejtekről (például Crick, 1989; Rubinov, 2015; Heeger, 2017). A biológiai agy tanul a munkahelyen, míg az ideghálózatoknak össze kell kapcsolódniuk, mielőtt felhasználhatók lennének. Ezenkívül, miután kiképezték, a mély hálózatok általában előre-előre számolnak, miközben a kéregben vannak fő visszatérő áramkörök. De ez egyszerűen tükrözi a mesterséges és valós neuronok különböző módjait. A mesterséges hálózatok egy fix feladatra vannak kiképezve, míg vizuális agyunknak meg kell birkóznia a változó környezettel és a feladatok igényeivel, így soha nem nő ki a tanulási képesség szükségessége. Ezenkívül a közelmúltban nagy előrelépés történt a képzett visszatérő ideghálózatok alkalmazásában mind számítási feladatokhoz, mind pedig idegi jelenségek magyarázataként (Barak, 2017).

Nem világos, tekintettel arra, amit tudunk a neuronokról és az idegi plaszticitásról, hogy a backprop hálózat megvalósítható-e biológiailag elfogadható áramkörök segítségével (de lásd: Mazzoni, Andersen és Jordan, 1991; Bengio, Le, Bornschein, Mesnard és Lin, 2015 ). Számos ígéretes erőfeszítés van azonban a biológiailag elfogadhatóbb tanulási szabályok megvalósítására, például a tüske-időzítéstől függő plaszticitás (Mazzoni et al., 1991; Bengio et al., 2015; Sacramento, Costa, Bengio és Senn, 2017).

A mérnökök és az informatikusok, bár a biológia ihlette, a gépi tanulási eszközök fejlesztésére összpontosítanak, amelyek megoldják a gyakorlati problémákat. Így az ezeken az eszközökön alapuló modellek gyakran nem tartalmazzák a fiziológia által előírt ismert korlátozásokat. Ehhez azt lehetne ellenkezni, hogy minden biológiai modell absztrakció, és hasznos lehet még akkor is, ha nem sikerül megragadni az élő szervezet minden részletét.

Néhány biológiai modellező panaszkodik, hogy az ideghálóknak riasztóan sok paraméterük van. A mély ideghálózatok továbbra is átlátszatlanok. A neurális hálózati modellezés előtt a modell egyszerűbb volt, mint az általa kifejtett adatok. A mély ideghálók jellemzően ugyanolyan összetettek, mint az adatok, és a megoldásokat nehéz vizualizálni (de lásd Zeiler & Fergus, 2013). Míg az edzéskészletek és a megtanult súlyok hosszú listák, a hálózat generatív szabályai (a számítógépes programok) rövidek. Ennek egyik íze a kéreg kaszkádos kánoni számításaira vonatkozó javaslatok (Hubel & Wiesel, 1962; Simoncelli & Heeger, 1998; Riesenhuber & Poggio, 1999; Serre, Wolf, Bileschi, Riesenhuber és Poggio, 2007). Hagyományosan a nagyon sok paraméter megléte gyakran túlterheléshez vezetett - vagyis az edzéskészlet jó teljesítményéhez és a rajta kívüli gyenge teljesítményhez -, de az áttörés az, hogy a nagy számú paraméterrel rendelkező mélyen tanuló hálózatok mégis jól általánosítanak. Ezenkívül a Bayes-i nemparametrikus modellek fegyelmezett megközelítést kínálnak a modellezéshez korlátlan számú paraméter mellett (Gershman & Blei, 2011). Mallat (2016) azt is megjegyzi, hogy a probléma ismert szimmetriái jelentősen csökkenthetik a megtanulandó paraméterek számát.

Egyes statisztikusok attól tartanak, hogy a szigorú statisztikai eszközöket elmélyíti a mély tanulás, amelyből hiányzik a szigor (Friedman, 1998; Matloff, 2014; de lásd: Breiman, 2001; Efron és Hastie, 2016). A feltételezéseket ritkán mondják el. Nincsenek konfidencia intervallumok a megoldáson. A teljesítmény azonban általában keresztellenőrzött, általánosítást mutat. A mély tanulás nem konvex, de bebizonyosodott, hogy a konvex hálózatok képesek kiszámítani a hátsó valószínűséget (pl. Rojas, 1996). Továbbá a gépi tanulás és a statisztikák közelednek egymáshoz, hogy általánosabb perspektívát nyújtsanak a szigorú valószínűségi következtetésekről (Chung, Lee és Sompolinsky, 2018).

Egyes fiziológusok megjegyzik, hogy az idegaktivitás dekódolása az inger helyreállítása érdekében érdekes és hasznos, de nem ismerteti az idegsejtek működését. Néhány vizuális pszichofizikus megjegyez néhány lényeges különbséget az emberi megfigyelők és a mély hálózatok teljesítménye között olyan feladatokban, mint a tárgyfelismerés és a kép torzulása (Ullman, Assif, Fetava és Harari, 2016; Berardino, Laparra, Ballé és Simoncelli, 2017). Néhány kognitív pszichológus elutasítja a mély ideghálózatokat, mivel nem képesek elsajátítani „a gyermekek által elvégzett alapvető dolgokat, mint például egy szabályos ige múlt idejének elsajátítását” (Marcus et al., 1992). A mély tanulás lassú. A természetes képeken lévő tárgyak felnőtt felismerési pontossággal történő felismeréséhez a korszerű mély neurális hálózathoz kategóriánként 5000 címkézett példa szükséges (Goodfellow, Bengio és Courville, 2016). De a gyerekeknek és a felnőtteknek csak 100 ismeretlen ábécé betűjére van szükségük ahhoz, hogy ugyanolyan pontosságot érjenek el, mint a folyékony anyanyelvű olvasók (Pelli et al., 2006). Ezeknek a kihívásoknak a leküzdése nem csupán mély tanulást igényel.

Ezek a jelenlegi korlátok arra késztetik a gyakorlókat, hogy fokozzák a mély tanulás körét és szigorát. De ne feledje, hogy a számítástechnika egyik legjobb osztályozóját a biológiai elvek inspirálták (Rosenblatt, 1958; LeCun, 1985; Rumelhart, Hinton és Williams, 1986; LeCun és mtsai, 1989; Riesenhuber és Poggio, 1999; és lásd LeCun, Bengio és Hinton 2015). Ezen osztályozók közül néhány olyan jó, hogy időnként meghaladja az emberi teljesítményt, és durva modellként szolgálhat a biológiai rendszerek osztályozásához (pl. Khaligh-Razavi & Kriegeskorte, 2014; Yamins és mtsai, 2014; Ziskind és mtsai, 2014; Testolin és mtsai., 2017).

Mérföldkövek a besorolásban

Matematika kontra mérnöki tudomány

A gépi tanulás történetének két szála van: a matematika és a mérnöki tudomány (2. ábra). A matematikai szálban két statisztikus, Fisher (1922) és később Vapnik (2013) dolgozott ki matematikai transzformációkat kategóriák kibontására. Eloszlásokat feltételeztek és bebizonyították a konvergenciát.