Bevezető útmutató a lineáris programozásról (törekvő) adatkutatók számára
Bevezetés
Az optimalizálás az életmód. Mindannyian rendelkezünk véges erőforrásokkal és idővel, és szeretnénk a lehető legtöbbet kihozni belőlük. Az idő produktív felhasználásától kezdve az ellátási lánc problémáinak megoldásához a vállalat számára - minden optimalizálást igényel. Különösen érdekes és releváns téma az adattudományban.
Ez egy nagyon érdekes téma - egyszerű problémákkal indul, de nagyon összetetté válhat. Például egy csokoládé megosztása a testvérek között egyszerű optimalizálási probléma. Nem matematikai szempontból gondolkodunk, miközben megoldjuk. Másrészt az e-tailer készlet- és raktározási stratégiájának kidolgozása nagyon összetett lehet. A különböző régiókban különböző népszerűségű SKU-k milliói meghatározott időben és erőforrásokban szállíthatók - érted, mire gondolok!
A lineáris programozás (LP) az optimalizálás egyik legegyszerűbb módja. Néhány egyszerűsítő feltételezéssel segít megoldani nagyon összetett optimalizálási problémákat. Elemzőként mindenképpen találkoznia kell olyan alkalmazásokkal és problémákkal, amelyeket a lineáris programozás segítségével kell megoldani.
Valamilyen oknál fogva az LP nem kap annyi figyelmet, mint amennyit megérdemel az adattudomány tanulása közben. Szóval, azt hittem, hadd tegyek igazságot ennek a fantasztikus technikának. Úgy döntöttem, hogy írok egy cikket, amely egyszerű angol nyelven magyarázza a lineáris programozást. A lehető legegyszerűbbé tettem a tartalmat. Az ötlet az, hogy elinduljon és izgatott legyen a lineáris programozással kapcsolatban.
jegyzet- Ha ezt kurzus formátumban szeretné megtanulni, akkor ezt az ingyenes kurzust kurátora az Ön számára- Lineáris programozás adattudományi szakembereknek
Tartalomjegyzék
- Mi a lineáris programozás?
- Alapfogalmak
- Az LP probléma meghatározásának folyamata
- Oldja meg a lineáris programot grafikus módszerrel
- Oldja meg a lineáris programot az R használatával
- Oldja meg a lineáris programot az OpenSolver segítségével
- Simplex módszer
- Északnyugati sarok módszer és legkisebb költség módszer
- A lineáris programozás alkalmazásai
1. Mi a lineáris programozás?
Mi az a lineáris programozás? A lineáris programozás egy egyszerű technika, ahol mi ábrázol összetett összefüggések lineáris függvényeken keresztül, majd megtalálják az optimális pontokat. Az előző mondat fontos szavát ábrázolják. A valós kapcsolatok sokkal összetettebbek lehetnek - de egyszerűsíthetjük lineáris kapcsolatokra.
A lineáris programozás alkalmazásai mindenütt körülötted vannak. Lineáris programozást használ személyes és szakmai fronton. Lineáris programozást használ, ha otthonról munkába jár, és a legrövidebb utat szeretné megtenni. Vagy ha van projektbemutatása, akkor stratégiákat készít annak érdekében, hogy a csapata hatékonyan működjön az időben történő szállítás érdekében.
Példa egy lineáris programozási problémára
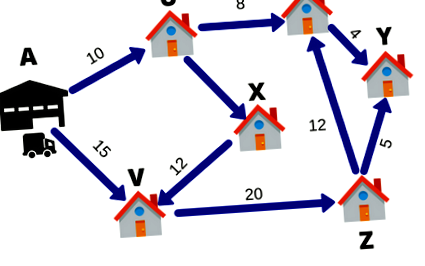
Tegyük fel, hogy egy FedEx kézbesítőnek 6 csomagot kell szállítania egy nap alatt. A raktár az A. pontban található. A 6 szállítási rendeltetési helyet U, V, W, X, Y és Z adja meg. A vonalakon lévő számok a városok közötti távolságot jelzik. Az üzemanyag és az idő megtakarítása érdekében a kézbesítő a legrövidebb utat akarja megtenni.
Tehát a kézbesítő kiszámítja a különböző útvonalakat, hogy mind a 6 célállomáshoz eljuthasson, majd előáll a legrövidebb útvonal. A legrövidebb útvonal kiválasztásának ezt a technikáját lineáris programozásnak nevezzük.
Ebben az esetben a kézbesítő célja, hogy a csomagot mind a 6 célállomáson időben kézbesítse. A legjobb útvonal kiválasztásának folyamatát Operációkutatásnak nevezzük. Az operációkutatás a döntéshozatal egyik megközelítése, amely a rendszer működtetésére szolgáló módszerek sorozatát foglalja magában. A fenti példában a rendszerem a Szállítási modell volt.
A lineáris programozást arra használjuk, hogy adott korlátok mellett a legoptimálisabb megoldást találjuk egy problémára. A lineáris programozás során a valós problémánkat matematikai modellvé formáljuk. Ez magában foglal egy objektív függvényt, lineáris egyenlőtlenségeket a korlátozások alatt.
A fenti 6 pont lineáris ábrázolása a valós világot reprezentálja? Igen és nem. Ez túl egyszerűsítés, mivel a valós útvonal nem egyenes lenne. Valószínűleg több fordulata, visszafordulása, jelzése és forgalmi dugója lesz. De egy egyszerű feltételezéssel drasztikusan csökkentettük a probléma összetettségét, és olyan megoldást hozunk létre, amelynek a legtöbb forgatókönyvben működnie kell.
Probléma megfogalmazása - Készítsünk néhány csokoládét
Példa: Vegyünk egy csokoládégyártó vállalatot, amely csak kétféle csokoládét gyárt - A és B. Mindkét csokoládéhoz csak Tej és Choco szükséges. Az A és B egységek gyártásához a következő mennyiségekre van szükség:
- Minden A egységhez 1 egység tej és 3 egység Choco szükséges
- Minden B egységhez 1 egység tej és 2 egység Choco szükséges
A vállalati konyhában összesen 5 egység tej és 12 egység csokoládé van. Minden értékesítéskor a társaság nyereséget termel
- 6 Rs eladott A egységenként
- Rs 5 eladott B egységenként.
Most a vállalat maximalizálni akarja profitját. Hány egységet kell előállítania A-ból és B-ből?
Megoldás: Az első dolog, hogy táblázatos formában képviselem a problémát a jobb megértés érdekében.
| Tej | Choco | Nyereség egységenként | |
| A | 1 | 3 | Rs 6 |
| B | 1 | 2 | Rs 5 |
| Teljes | 5. | 12. |
Legyen az A által előállított egységek száma = X
Legyen a B által előállított egységek száma = Y
Most a teljes nyereséget Z képviseli
A vállalat által elért teljes nyereséget a megtermelt A és B egységek összesített számának szorzatával számolva, egységenként 6, illetve 5 egységnyi nyereséggel.
Nyereség: Max Z = 6X + 5Y
ami azt jelenti, hogy maximalizálnunk kell a Z-t.
A vállalat megpróbálja minél több A és B egységet előállítani a profit maximalizálása érdekében. De a Milk és a Choco források korlátozott mennyiségben állnak rendelkezésre.
A fenti táblázat szerint minden A és B egységhez 1 egység tej szükséges. A rendelkezésre álló tej teljes mennyisége 5 egység. Ezt matematikailag ábrázolni,
X + Y ≤ 5
Ezenkívül minden A és B egységhez 3 egység és 2 egység Choco szükséges. A rendelkezésre álló Choco teljes mennyisége 12 egység. Ezt matematikailag ábrázolni,
3X + 2Y ≤ 12
Az A egységek értékei csak egész számok lehetnek.
Tehát van még két korlátozásunk, X ≥ 0 és Y ≥ 0
A vállalat maximális profit elérése érdekében a fenti egyenlőtlenségeket ki kell elégíteni.
Ezt nevezzük egy valós probléma matematikai modellvé történő megfogalmazásának.
A lineáris programozásban használt általános terminológiák
Határozzuk meg a Linear Programming néhány terminológiáját a fenti példa segítségével.
- Döntési változók: A döntési változók azok a változók, amelyek meghatározzák a kimenetemet. Ők jelentik a végső megoldásomat. Bármely probléma megoldásához először meg kell határoznunk a döntési változókat. A fenti példában az A és B egységek összesített száma, amelyet X és Y jelöl, illetve az én döntési változóim.
- Objektív funkció: A döntéshozatal célkitűzésként definiálják. A fenti példában a vállalat növelni kívánja a Z által képviselt teljes profitot. Tehát a profit a célom.
- Korlátok: A korlátok a döntési változókra vonatkozó korlátozások vagy korlátozások. Általában korlátozzák a döntési változók értékét. A fenti példában a Tej és a Choco erőforrások rendelkezésre állásának korlátozása a korlátom.
- Nem negatív korlátozás: Minden lineáris program esetében a döntési változóknak mindig nem negatív értékeket kell felvenniük. Ez azt jelenti, hogy a döntési változók értékének nagyobbnak vagy egyenlőnek kell lennie, mint 0.
A lineáris programozási probléma megfogalmazásának folyamata
Nézzük meg a lineáris programozási probléma általános meghatározásának lépéseit:
- Határozza meg a döntési változókat
- Írja le a célfüggvényt
- Említse meg a korlátozásokat
- Pontosan mondja ki a nem negativitás korlátozását
Ahhoz, hogy egy probléma lineáris programozási probléma legyen, a döntési változóknak, a célfüggvényeknek és a korlátozásoknak mind lineáris függvényeknek kell lenniük.
Ha mindhárom feltétel teljesül, akkor a Lineáris programozási probléma.
2. Oldja meg a lineáris programokat grafikus módszerrel
A lineáris program több módszerrel is megoldható. Ebben a szakaszban megvizsgáljuk a grafikus módszert egy lineáris program megoldására. Ezzel a módszerrel kétváltozós lineáris programot lehet megoldani. Ha csak két döntési változója van, akkor az optimális megoldás megtalálásához használja a grafikus módszert.
A grafikus módszer magában foglalja a korlátozásoknak megfelelő lineáris egyenlőtlenségek halmazának megfogalmazását. Ezután az egyenlőtlenségeket egy X-Y síkra ábrázoljuk. Miután az összes egyenlőtlenséget ábrázoltuk egy grafikonon, a metsző régió kivitelezhető régiót ad nekünk. A megvalósítható régió elmagyarázza, hogy modellünk milyen értékeket vehet fel. És ez az optimális megoldást is megadja nekünk.
Értsük meg ezt egy példa segítségével.
Példa: Egy gazda a közelmúltban 110 hektáros földterületet szerzett. Úgy döntött, hogy ezen a földön búzát és árpát fog termeszteni. A nap minősége és a régió kiváló éghajlata miatt a búza és az árpa teljes termelése értékesíthető. Meg akarja tudni, hogyan kell az egyes fajtákat a 110 hektárra ültetni, figyelembe véve a költségeket, a nettó nyereséget és a munkaigényt az alább látható adatok szerint:
| Fajta | Költség (ár/hec) | Nettó nyereség (ár/hec) | Embernapok/Hec |
| Búza | 100 | 50 | 10. |
| Árpa | 200 | 120 | 30 |
A gazdálkodó költségvetése 10 000 USD, a tervezési időszakban pedig 1200 embernap áll rendelkezésre. Keresse meg az optimális megoldást és az optimális értéket.
Megoldás: Ennek a problémának a megoldásához először megfogalmazzuk a lineáris programunkat.
Lineáris probléma megfogalmazása
1. lépés: Határozza meg a döntési változókat
A búza termesztésének teljes területe = X (hektárban)
Az árpa termesztésének teljes területe = Y (hektárban)
X és Y a döntési változóim.
2. lépés: Írja meg a célfüggvényt
Mivel a teljes földterületről származó termelés eladható a piacon. A gazda teljes termelésének maximális hasznát szeretné elérni. A búza és az árpa nettó nyereséget kapunk. A gazdálkodó nettó nyeresége 50 amerikai dollár minden búzahektáron és 120 dollár minden árpa után.
Célfüggvényünk (amelyet Z adott), Max Z = 50X + 120Y
3. lépés: A korlátok megírása
1. A gazdálkodó teljes költségvetése 10 000 USD. A búza és az árpa hektáronkénti előállítási költségeit szintén megadják nekünk. Van egy felső korlát a gazdálkodó által elköltött összes költségre. Tehát az egyenletünk:
100X + 200Y ≤ 10 000
2. A következő megkötés az embernapok számának rendelkezésre állásának felső korlátja a tervezési horizonton. A rendelkezésre álló embernapok száma összesen 1200. A táblázat szerint a búza és az árpa hektáronkénti embernapjait kapjuk.
10X + 30Y ≤ 1200
3. A harmadik korlát az ültetvények teljes területe. A teljes rendelkezésre álló terület 110 hektár. Tehát az egyenlet lesz,
X + Y ≤ 110
4. lépés: A nem negativitás korlátozása
X és Y értéke 0-nál nagyobb vagy egyenlő lesz. Ez magától értetődik.
X ≥ 0, Y ≥ 0
Megfogalmaztuk lineáris programunkat. Ideje megoldani.
LP megoldása grafikus módszerrel
Mivel tudjuk, hogy X, Y ≥ 0. Csak az első negyedet vesszük figyelembe.
A fenti egyenletek grafikonjának ábrázolásához először leegyszerűsítem az összes egyenletet.
100X + 200Y ≤ 10 000 egyszerűsíthető X + 2Y ≤ 100-ra, ha elosztjuk 100-mal.
10X + 30Y ≤ 1200 egyszerűsíthető X + 3Y ≤ 120-ra 10-gyel elosztva.
A harmadik egyenlet egyszerűsített formában van, X + Y ≤ 110.
Ábrázolja az első 2 sort egy grafikonon az első negyedben (az alábbiak szerint)
Az optimális megvalósítható megoldást abban a metszéspontban érik el, ahol a költségvetés és az embernapok korlátai aktívak. Ez azt jelenti, hogy az X + 2Y ≤ 100 és X + 3Y ≤ 120 egyenletek metszéspontja az optimális megoldást nyújtja.
Az optimális megoldást adó X és Y értékek (60,20).
A profit maximalizálása érdekében a mezőgazdasági termelőnek búzát és árpát kell termelnie 60 hektáron, illetve 20 hektár földön.
A vállalat által elért maximális nyereség,
Max Z = 50 * (60) + 120 * (20)
Jegyzet: Mindent, amit itt tanítottak, tanfolyam formátumban is tanították ebben az ingyenes kurzusban - Lineáris programozás az adattudományi szakemberek számára
3. Oldja meg a lineáris programot az R használatával
Az R egy nyílt forráskódú eszköz, amely az adatkutatók körében nagyon népszerű az alapvető adattudományi feladatok elvégzésében. A lineáris programozás nagyon egyszerű, és csak néhány lépésben érhetünk el optimális megoldást. Gyere, tanuljunk.
Példa: Egy játékgyártó szervezet kétféle A és B játékot állít elő. Mindkét játékot 25, 20, 20 dollárért árulják. Naponta 2000 erőforrás áll rendelkezésre, amelyekből az A játék 20 egységet igényel, míg a B játék 12 egységet igényel. Mindkét játék gyártási ideje 5 perc. A teljes munkaidő napi 9 óra. Mennyi legyen az egyes csövek gyártási mennyisége a profit maximalizálása érdekében?
A célfüggvény a következő:
Max. Z = 25x + 20y
ahol x az A cső egységei
y a B cső egységei
Korlátok:
20x + 12y opciók-> bővítmények-> válassza a megoldót-> kattintson a kezelés-> válassza a megoldót-> kattintson az OK gombra. Megoldója most hozzáadva az excelben. Az Adatok fül alatt ellenőrizheti.
Az első dolog, amit be fogok tenni, az adatok beírása az Excelbe. Az adatok excelbe történő beírása után kiszámoltam a C3: F3 összértékét. Hasonlóan mások számára is. Ez azért történik, hogy a Silo 1 és mások teljes igényét elvigye.
Ezek után kettéválasztom a modellemet. Az első táblázat megadja a szállított egységeket, a második táblázat pedig az egységköltségeket.
Most kiszámolom a teljes költségemet, amelyet az egységköltség és a szállított egységek Sumproduct ad meg.
Most a Solver segítségével fogom kiszámítani a modellemet. Hasonló a fenti módszerhez. Adja hozzá a célfüggvényt, a változó cellákat, a kényszereket.
Most a modell készen áll a megoldásra. Kattintson a megoldásra, és megkapja az optimális költséget. A minimális szállítási költség 435 USD.
7. A lineáris programozás alkalmazásai
A lineáris programozást és az optimalizálást különböző iparágakban használják. A feldolgozóipar és a szolgáltatóipar rendszeresen használja a lineáris programozást. Ebben a részben a lineáris programozás különféle alkalmazásait vizsgáljuk meg.
Nos, a lineáris programozás alkalmazásai itt nem érnek véget. A lineáris programozásnak még sok más alkalmazása létezik a valóságban, például a részvényesek, a sport, a tőzsdék stb. Által. Folytassa és fedezze fel tovább.
Végjegyzetek
Remélem tetszett olvasni ezt a cikket. Megpróbáltam megmagyarázni az összes alapfogalmat a lineáris programozás alatt. Ha bármilyen kétsége van vagy kérdése van, nyugodtan tegye meg őket a megjegyzések részben. Az egyszerű megértés érdekében ezt a hosszú cikket rövidebb tanfolyamformátumra bontottuk - Linear Programming for Data Science Professionals
Valamennyi fogalmat valóságos példával magyaráztam. Szeretném, ha kipróbálnád őket a végén, és gyakorlati tapasztalatokat szereznél. Tudasd velem mire gondolsz!
- Lineáris programozás és egészséges étrend - 2. rész; Matematika ∩ programozás
- Az újszülöttek, az elválasztott és a serdülő Wistar patkányok magas zsírtartalmú programozására adott szigetsejt-válasz
- Az anyák terhesség alatti programozása hosszú távú szülés utáni elhízást vált ki egérkutatásban,
- Keto Plateau Miért NEM A Fogyás NEM Lineáris Folyamat KetoVale
- Hafthor Bjornsson; s Hegyvidéki étrend izom; Fitness