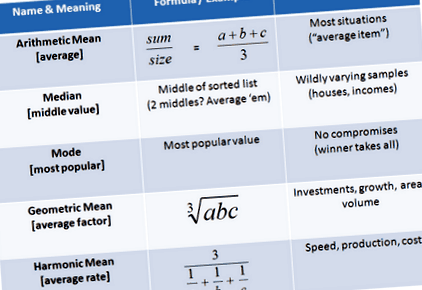
Az adatok elemzése az átlag felhasználásával

Az átlag egyszerű jelentés, többféle jelentéssel. A használandó átlag típusa attól függ, hogy összeadja-e, szorozza-e, csoportosítja-e vagy osztja-e a munkát a készlet elemei között.

Gyors kvíz: 30 km/h-val vezetett dolgozni, 60 km/h-val pedig vissza. Mi volt az átlagos sebességed?

Tipp: Nem 45 mph, és nem számít, milyen messze van az ingázás. Olvassa el, hogy megértse ennek a statisztikai eszköznek a sok alkalmazását.

De mit jelent ez?

Lépjünk vissza egy kicsit: miről szól az „átlag”?

Legtöbbünk számára ez a „középen lévő szám” vagy egy „kiegyensúlyozott” szám. Rajongok a multipleviewpointokért, ezért íme az átlag egy másik értelmezése:

Az átlag az az érték, amely minden meglévő elemet felválthat, és ugyanaz az eredmény. Ha eldobhatnám az adataimat, és egy „átlagos” értékre cserélhetném, akkor mi lenne az?

Az átlag egyik célja egy adatkészlet megértése egy „reprezentatív” minta megszerzésével. De a számítás attól függ, hogy a csoport elemei hogyan hatnak egymásra. Lássuk.

A számtani átlag

A számtani átlag a leggyakoribb átlagtípus:

Tegyük fel, hogy súlya 150 font, és liftben van, 100 kg-os gyerekkel és 350 kg-os rozmárral. Mi az átlagos súly?

Az igazi kérdés az, hogy "Ha ezt a vidám csoportot 3 azonos emberre cserélné, és ugyanazt a terhelést szeretné a liftben, akkor mit kell mérnie az egyes klónoknak?"

Ebben az esetben három embert cserélnénk, akik mindegyike 200 font ([150 + 100 + 350)/3], és senki sem lenne a bölcsebb.

Jól működik azoknál a listáknál, amelyeket egyszerűen kombinálnak (hozzáadnak).
Könnyen kiszámítható: csak adja hozzá és ossza fel.
Intuitív - ez a „középen” lévő szám, amelyet nagy értékek húznak fel, és kisebbek hoznak le.

Az átlagot torzíthatják a kiugró értékek - ez nem jár jól a vadul változó mintákkal. A 100, 200 és -300 átlag 0, ami félrevezető.

A számtani átlag az idő 80% -ában remekül működik; sok mennyiséget összeadunk. Sajnos mindig előfordul a helyzeteknek az a 20% -a, ahol az átlag nem egészen illik.

Középső

A medián a „középen lévő elem”. De az átlag (számtani átlag) nem ugyanazt jelenti? Mi ad?

Humorozz egy pillanatra: mi a „közepe” ezeknek a számoknak?

Nos, 3 a lista közepe. És bár az átlag (22) valahol a „középen” van, a 22 nem igazán képviseli az eloszlást. Valószínűbb, hogy egy számot közelebb kapunk a 3-hoz, mint a 22-höz. Az átlagot 100-mal húzták fel, egy szélsőérték.

A medián megoldja ezt a problémát a számot a rendezett lista közepén. Ha két középső szám van (páros tételszám), vegye csak az átlagukat. A 100-hoz hasonló kiugró értékek csak a mediánt húzzák végig a rendezett lista egy elemén, ahelyett, hogy drasztikusan változtatnának: az 1 2 3 4 mediánja 2,5.

Jól kezeli a kiugró értékeket - gyakran a csoport legpontosabb ábrázolása
Az adatokat két csoportra osztja, mindegyik azonos elemszámmal rendelkezik

Nehezebb lehet kiszámítani: először össze kell rendeznie a listát
Nem olyan közismert; amikor azt mondod, hogy „medián”, akkor az emberek azt gondolhatják, hogy „átlagos”

Néhány poén a következőképpen szól: „Az összes sofőr fele alacsonyabb az átlagnál. Ijesztő, nem? ”. De valójában a fejedben tudod, hogy azt kellene mondaniuk, hogy "az összes sofőr fele medián alatt van".

Az olyan számokat, mint a lakásárak és a jövedelmek, gyakran a mediánban adják meg, mivel erről ötletet akarunk a csomag közepe. Bill Gates, aki néhány milliárd plusz egy évet keres, megdöntheti az átlagos jövedelmet, de ez nem releváns abban, hogy hogyan változott a rendes ember bére. Nem érdekel bennünket a jövedelmek vagy a lakásárak „összeadása” - csak a középsőt akarjuk megtalálni.

A használt átlag típusa ismét az adatok felhasználásától függ.

A mód furcsán hangzik, de csak annyit jelent szavazzon. És néha a szavazás, nem a számítás a legjobb módja kap egy reprezentatív mintát amiről az emberek vágynak.

Tegyük fel, hogy bulit rendez, és választania kell egy napot (1 hétfő, 7 vasárnap). A „legjobb” nap az a lehetőség lenne, amely a legtöbb embert kielégíti: az átlagnak nincs értelme. ("Bob szereti a pénteket, Alice pedig a vasárnapot? Szombat van!").

Hasonlóképpen számokkal mérhetők a színek, a filmbeállítások és még sok minden más. De megint az ideális választás lehet a mód, nem pedig az átlag: az „átlagos” színes vagy az „átlagos” film lehet… nem kielégítő (Rambo találkozik a büszkeséggel és balítélettel).

Jól működik exkluzív szavazási helyzeteknél (ez vagy ez a választás; nincs kompromisszum)
Olyan választást ad, amelyet a legtöbb ember vágyott (míg az átlag olyan döntést adhat, amelyet senki sem akart).
Egyszerű megérteni

Több erőfeszítést igényel a számításhoz (össze kell számolni a szavazatokat)
„A győztes mindent megtesz” - nincs középső út

A „mód” kifejezés nem annyira elterjedt, de most már tudod, milyen gombra kell figyelni, amikor a kedvenc statisztikai programoddal játszol.

Geometriai átlag

Az „átlagos elem” attól függ, hogy miként használjuk a meglévő elemeinket. Legtöbbször a tételek összeadódnak, és a számtani átlag jól működik. De néha többet kell tennünk. A beruházások, a terület és a volumen kezelésénél nem adunk hozzá tényezőket, hanem szorozzuk azokat.

Próbáljunk ki egy példát. Melyik portfóliót részesíti előnyben, azaz melyiknél jobb tipikus év?

A portfólió: + 10%, -10%, + 10%, -10%
B portfólió: + 30%, -30%, + 30%, -30%

Elég hasonlóak. Mindennapi átlagunk (számtani átlag) azt mondja, hogy mindketten hullámvasutak, de nulla nyereséget vagy veszteséget kell átlagolniuk. És talán B jobb, mert úgy tűnik, hogy a jó években többet nyer. Jobb?

Wrongo! Az ilyen beszéd megégeti a tőzsdén: a befektetési hozamok megsokszorozódnak, nem pedig hozzáadódnak! Nem lehetünk akarva-akaratlanok, és használhatjuk a számtani átlagot - meg kell találnunk a tényleges megtérülési rátát:

A portfólió:
- Megtérülés: 1,1 *, 9 * 1,1 *, 9 =, 98 (2% -os veszteség)
- Éves átlag: (.98) ^ (1/4) = 0,5% -os veszteség évente (ez körülbelül 2%/4, mert a számok kicsiek).
B portfólió:
- 1,3 *, 7 * 1,3 *, 7 =, 83 (17% -os veszteség)
- Éves átlag: (.83) ^ (1/4) = évi 4,6% -os veszteség.

2% vs 17% veszteség? Ez hatalmas különbség! Mindkét portfóliótól távol maradnék, de ha kényszerítenék, az A-t választanám. Nem tudjuk csak összeadni és megosztani a hozamokat - az exponenciális növekedés nem így működik.

Néhány további példa:

Inflációs ráta: Ön inflációja 1%, 2% és 10%. Mekkora volt az átlagos infláció ez idő alatt? (1,01 * 1,02 * 1,10) ^ (1/3) = 4,3%
Kuponok: Van kuponja 50%, 25% és 35% kedvezménnyel. Feltéve, hogy mindet felhasználhatja, mekkora az átlagos kedvezmény? (azaz milyen szelvényt lehetne háromszor felhasználni?). (, 5 *, 75 *, 65) ^ (1/3) = 37,5%. Gondoljon a kuponokra, mint „negatív” hozamra - amúgy az áruház számára.
Terület: Van egy 40 × 60 yardos telek. Mi az „átlagos” oldal - vagyis mekkora lenne a megfelelő négyzet? (40 * 60) ^ (0,5) = 49 yard.
Hangerő: Van egy 12 × 24 × 48 hüvelykes szállítódoboza. Mi az „átlagos” méret, vagyis mekkora lenne a megfelelő kocka? (12 * 24 * 48) ^ (1/3) = 24 hüvelyk.

Biztos vagyok benne, hogy még sok példát talál: a geometriai átlag megtalálja a „tipikus elemet”, amikor az elemeket összeszorozzuk. Fog egy számkészletet, megszorozza őket, és megkapja az N-edik gyököt (ahol N az Ön által figyelembe vett elemek száma).

Sokáig azon gondolkodtam, miért hasznos a geometriai középérték - most már tudjuk.

Harmonikus átlag

A harmonikus középértéket nehezebb vizualizálni, de mégis hasznos. (Egyébként a „harmonikusok” olyan számokra utalnak, mint 1/2, 1/3 - 1, bármi felett.) A harmonikus átlag segít kiszámítani átlagos arányok amikor több elem együtt dolgozik. Lássuk.

Ha 30 mph sebességem van, akkor ez azt jelenti, hogy minden bemenetre (1 óra vezetésre) kapok valamilyen eredményt (30 mérföldet megyek). A többszörös (X & Y) hatások átlagolásakor a kimenetekre és a bemenetekre kell gondolni, nem a nyers számokra.

átlagos arány = teljes kimenet/teljes bevitel

Ha egy projektre mind X-et, mind Y-t feltesszük, mindegyik ugyanannyi munkát végez, akkor mekkora az átlagos arány? Tegyük fel, hogy X 30 mph és Y 60 mph. Ha nekünk hasonló feladatokat kell elvégeznünk (mérföldet kell megtennünk), akkor az érvelés a következő:

X 1/X időt vesz igénybe (1 mérföld = 1/30 óra)
Y 1/Y időt vesz igénybe (1 mérföld = 1/60 óra)

A be- és kimenetek kombinálásával kapjuk:

Teljes kimenet: 2 mérföld (X és Y egyenként 1 ”-et tesznek ki)
Összes bemenet: 1/X + 1/Y (mindegyik más-más időt vesz igénybe; képzeljen el egy váltóversenyt)

Az átlagos kimeneti/bemeneti ráta pedig:

Ha 3 elemünk lenne a keverékben (X, Y és Z), az átlagos arány a következő lenne:

Nagyon jó, hogy ezt a parancsikont használjuk ahelyett, hogy minden alkalommal elvégeznénk az algebrát - még az 5 arány átlagának megtalálása sem olyan rossz. Példánkkal 30 km/h sebességgel mentünk dolgozni, és 60 km/h sebességgel jöttünk vissza. Az átlagos sebesség megállapításához csak a képletet használjuk.

De nem kell tudnunk, milyen messze van a munka? Dehogy! Nem számít, milyen hosszú az útvonal, X és Y azonos kimenettel rendelkezik; vagyis R mérföldet haladunk X sebességgel, és további R mérföldet Y sebességgel. Az átlagos sebesség megegyezik azzal, hogy 1 mérföldet haladunk X sebességgel és 1 mérföldet Y sebességgel:

Van értelme, ha az átlagot a lassabb sebesség felé torzítják (közelebb a 30-hoz, mint 60-hoz). Végül is kétszer annyi időt töltünk 30 km/h sebességgel, mint 60 km/h: ha a munka 60 mérföldnyire van, akkor 2 óra van ott és 1 óra vissza.

Fő ötlet: A harmonikus átlagot akkor alkalmazzák, ha két ráta járul hozzá ugyanahhoz a munkaterheléshez. Minden árfolyam a váltóverseny és ugyanannyit járulnak hozzá a kimenethez. Például egy oda-vissza utat teszünk meg munkába és vissza. Az eredmény fele (megtett távolság) az első sebességtől (30 km/h), a másik fele pedig a második sebességtől származik (60 mph).

A gótka: Ne feledje, hogy az átlag igen egyetlen elem, amely minden elemet felvált. Példánkban 40 km/h-val haladunk odafelé (30 helyett), 40 km/h-val pedig visszafelé (60 helyett). Fontos megjegyezni, hogy az egyes „szakaszokat” az átlagos arányra kell cserélnünk.

Adatátvitel: Adatokat küldünk kliens és szerver között. Az ügyfél 10 gigabájt/dollár, a szerver pedig 20 gigabájt/dollár sebességgel küld adatokat. Mi az átlagos költség? Nos, átlagosan 2/(1/10 + 1/20) = 13,3 gigabájt/dollár minden részre. Vagyis felcserélhetnénk az ügyfelet és a szervert két gépre, amelyek ára 13,3 gb/dollár. Mivel az adatokat elküldjük és fogadjuk is (mindegyik rész a „fele munkát” végzi), a valódi arányunk 13,3/2 = 6,65 gb/dollár.

Gépi termelékenység: Van egy gépünk, amelynek el kell készítenie és befejeznie az alkatrészeket. Előkészítéskor 25 modul/óra sebességgel fut. Befejezéskor 10 widget/óra sebességgel fut. Mi az általános arány? Nos, átlagosan 2/(1/25 + 1/10) = 14,28 widget/óra az egyes szakaszokhoz. Vagyis a meglévő időket két, 14,28 widget/óra sebességgel futó fázisra cserélhetnék ugyanazon hatás érdekében. Mivel egy alkatrész mindkét fázison megy keresztül, a gép 14,28/2 = 7,14 widgetet/óra teljesít.

Részvények vásárlása. Tegyük fel, hogy havonta 1000 dollár értékű részvényeket vásárol, nem számít az ár (dollárköltség átlagban). Januárban 25 USD/részvény, februárban 30 USD/részvény és márciusban 35 USD/részvény fizet. Mennyit fizettek az átlagárak? 3/(1/25 + 1/30 + 1/35) = \ 29,43 USD (mivel többet vásárolt alacsonyabb áron, és kevesebbet a drágábbnál). És 3000 $/29,43 = 101,94 részvényed van. A „terhelés” kissé elvont - a dollárokat részvényekké változtatja. Néhány hónap több dollárt használ fel részvény vásárlásához, mint mások, és ebben az esetben a magas arány rossz.

Ismét a harmonikus középérték segít mérni aránya ugyanazon az eredményen dolgozik együtt.

Yikes, ez trükkös volt

A harmonikus átlag trükkös: ha van különálló 10 alkatrész/óra és 20 alkatrész/óra sebességgel működő gépek, akkor az átlagos értéke 15 alkatrész/óra, mivel minden gép független, és Ön a képességek hozzáadása. Ebben az esetben a számtani átlag rendben működik.

Néha jó kétszer ellenőrizni, hogy a matematika jól működik-e. A géppéldában állításunk szerint 7,14 widgetet gyártunk óránként. Ok, mennyi időbe telik a 7.14 kütyü elkészítése?

Előkészítés: 7,14/25 =, 29 óra
Befejezés: 7,14/10 =, 71 óra

És igen, .29 + .71 = 1, tehát a számok beválnak: 1 óra szükséges 7.14 kütyü elkészítéséhez. Ha kétségei vannak, próbáljon meg néhány példát futtatni, hogy megbizonyosodjon arról, hogy az átlagos arány valóban az, amit kiszámított.

Következtetés

Még egy olyan egyszerű ötletnek is, mint az átlag, sok felhasználási lehetősége van - több olyan felhasználás van, amelyre még nem terjedt ki (súlypont, súlyozott átlagok, várható érték). A legfontosabb pont ez:

Az „átlagos elem” olyan tételnek tekinthető, amely helyettesítheti az összes többit
Az átlag típusa a meglévő elemek felhasználásától függ (Hozzáadva? Szorozva? Díjakként használva? Exkluzív lehetőségként használva?)

Meglepett, hogy a különböző típusú átlagok mennyire voltak hasznosak és változatosak az adatok elemzéséhez. Boldog matek.

Csatlakozzon több mint 450 ezer havi olvasóhoz

Élvezze a cikket? Rengeteg további segítséget nyújt a matematika tartós és intuitív megértésében. Csatlakozzon a hírlevélhez a bónusz tartalomért és a legújabb frissítésekért.