Diet Dietworks: Vékony paraméterek a zsírgenomikához, Romero és mtsai. 2017

Ez a cikk egy okos trükköt mutat be, amely jelentősen lerövidíti a paraméterek méretét.

Probléma: A genomikai adatok kezelésénél túl kevés példa van ($ O (10 ^ 3) $) a változó mérethez képest, amely általában $ O (10 ^ 6) $ nagyságrendű. Ez azért probléma, mert egy ilyen hatalmas változó méret mellett ez egy hatalmas paramétermérettel rendelkező modellnek fog megfelelni. De csak kevés képzési példánk van, ami miatt a modell nagyon könnyen illeszkedik az edzéskészlethez.

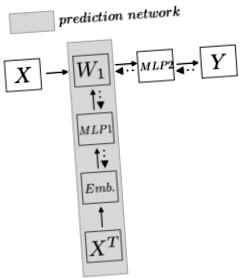
Módszer: Először formáljuk meg a problémákat, hogy tisztább képet kapjunk. Tegyük fel, hogy $ N $ x $ N_d $ méretű ($ N $ minták és $ N_d $ jellemzők/SNP-k) genomikai adatokkal rendelkezünk, ahol $ N \ ll N_d $. Meg akarunk tervezni egy modellt annak megjóslására, hogy egy mintának van-e bizonyos vonása. Ebben a cikkben a népesség rétegződése. Ahelyett, hogy közvetlenül alkalmaznánk a képzési példa tetejére a lineáris réteget, amely bizonyosan $ W_1: N_d $ x $ N_h $ méretű paraméterekkel jár, a szerző egy másik hálózat használatát javasolja a paraméterek előrejelzéséhez, ily módon a $ W_1 $ nem egy paraméter, de a paraméterek hálózatának jóslata. A következő grafikon egyértelműbben szemlélteti az ötletet:

vékony

A felső horizont hálózat a hagyományos modell, ahol a $ W_1 $ hatalmas méretekkel rendelkező paraméter, és túlterheléshez vezet. A szerző egy predikciós hálózatot (a szürke területet) használ a paraméter előrejelzéséhez. A predikciós hálózat először a teljes képzési adatkészletet transzponálja, és a funkciók mentén beágyazást kódol. Majd miután ezt a szolgáltatást betáplálta egy többszintű Preceptronba (MLP), a hálózat kiadja a súlyt. Tehát a predikciós hálózat minden edzés lépésben megjósolja a $ W_1 $ értéket, majd a $ X_n $ képzési példa ezt a $ W_1 $ értéket veszi fel, és rejtett ábrázolást kap, majd a normál lépéseket, azaz az MLP-t, majd a softmax-ot írja meg Y $. Ezután a hátralévő lépésben a veszteség visszajut a $ W_1 $ -ra és a jóslási hálózat többi részére.

Tehát miért működik az előrejelző hálózat, és miért csökken a paraméter mérete?

Először a szerző átadja a képzési adatkészletet a $ X ^ T \ fájlba N_d $ x $ N $ formátumban. Így minden sor tartalmazza a szolgáltatás minden mintájának adatait. Intuitív módon rögzít minden SNP-re vonatkozó információt. Tehát a beágyazás úgy alakítható ki, hogy a legjobban megragadja ennek a szolgáltatásnak a lényegét. Ez a cikk a beágyazások kódolásának több módszerét használja: randomizált, SNP2Vec, osztályonkénti hisztogram és képzett end-to-end. Tegyük fel, hogy minden funkciót $ N_f $ dimenzióba kódolunk, most pedig $ N_d $ x $ N_f $ méretet kapunk. Vegye figyelembe, hogy ez nem egy paraméter, hanem inkább egy edzéskészlethez hasonló.

A beágyazási lépés után MLP-t alkalmaztunk a tetején. Itt jön be a paraméterek levonása. Most úgy gondolhatjuk, hogy van egy képzési készletünk, amelynek minden példájához $ 1 $ x $ N $ $. Ezután kiképezhetünk egy $ N_f $ x $ N_h $ paraméter méretű MLP-t, hogy megkapjuk a $ 1 $ x $ N_h $ méret előrejelzését. Vegye figyelembe, hogy itt a paraméter mérete $ N_f $ x $ N_h $. Ezután minden $ N_d $ jellemző példát kiszámítva ezen a $ N_f $ x $ N $ H_h $ súlyon keresztül megkapjuk a $ N_d $ x $ N_h $ méretre vonatkozó jóslatunkat, amely akkora, mint $ W_1 $. Alapvetően $ (W_1) _j = \ phi (e_j) $, ahol $ e_j $ a $ j th $ szolgáltatás beágyazását jelenti.

Ezután közvetlenül megsokszorozzuk az eredeti $ X $ adatkészlet valódi képzési példáját a $ W_1 $ -val, majd több réteg neurális hálózatot és softmax-ot alkalmazunk minden konkrét feladatra. A hátsó terjedés a hibajelet a $ MLP1 $ -ba továbbítja, ahol a $ MLP1 $ súlyok egyre jobbak lesznek a $ W_1 $ előrejelzés beállításához.

Most készen vagyunk. Például GWAS-adatokkal foglalkozom, amelyeknek körülbelül $ N_d = 1 * 10 ^ 6 $ és $ N = 6000 $ adatkészlete van. Tegyük fel, hogy az első rétegben rejtett ábrázolást akarunk a $ N_h = 100 $ méretből. Tehát e hálózat nélkül a paraméter mérete $ 1 * 10 ^ 8 $. Tegyük fel, hogy most a hálózattal beágyazásunk $ N_f = 500 $ méretű, majd a network paraméter paramétere $ N_f $ x $ N_h = 5 * 10 ^ 4 $. Ez 2000 dollár szorzóval csökkenti a hálózati paraméter méretét.

Ez a cikk szintén nagy eredményt jelent a népesség rétegződésének téves osztályozásában, sok hagyományos megközelítést meghaladva.

A cikk érdekessége, hogy ha bármely paraméter mérete túl nagy, alkalmazhatjuk ezt a technikát, amely alapvetően egy kisebb tömegű közbenső ágenst vezet be, és a nagy méretű súlyt jóslási problémának tekinti. Ha rekonstruálni akarjuk az adatokat a VAE-ben vagy valamiben, akkor ezt a technikát alkalmazhatjuk a végső réteg súlyának csökkentésére is. Ez szépen megkerüli a túlterhelési problémát is, mivel most a $ W_1 $ súly a beágyazások gazdag ábrázolásából származik.