Pontos analitikai megoldás az állandó beszivárgáshoz az ülő Vízalapból egy alacsonyan áteresztő alrétegbe: Kirkham-Brock öröksége áttekintve

Talaj-, víz- és agrármérnöki tanszék, Qaboos szultán egyetem, Muscat, Omán

Matematikai és Mechanikai Intézet, Kazan Szövetségi Egyetem, Kazan, Oroszország

Talaj-, víz- és agrármérnöki tanszék, Qaboos szultán egyetem, Muscat, Omán

Matematikai és Mechanikai Intézet, Kazan Szövetségi Egyetem, Kazan, Oroszország

Absztrakt

1. Bemutatkozás

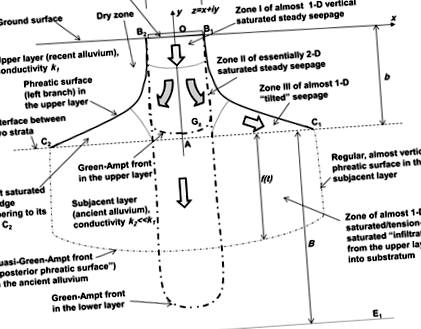
Az áramlási tartomány függőleges keresztmetszete a talajcsatornából egy nagyon áteresztő rétegbe szivároghat át, amely alacsonyan áteresztő aljzatot takar.

a) Átmeneti függőleges keresztmetszetek Bouwer [2002] az eltömődött és eltömődés nélküli mederágyakból behatolatlan vízalatti rétegbe való beszivárgás rendszerei, amelyek alul fekvő, át nem eresztő alapkőzetet tartalmaznak; b) kör alakú háromszög a hodográfban, amely megfelel az áramlási tartomány jobb felének az 1. ábra fizikai síkságán; (c) komplex potenciális tartomány; d) kiegészítő félsík.

Khan és mtsai. [1976, 1. ábra] és Borz [1982, 1. ábra], a továbbiakban rövidítve KB—Kirkham és Brock, az eldugult meder olyan MAR-rendszereinek tekintették, hogy egy adott akkréciós intenzitással táplált talajvíz-halmok egy stabil vízszinttel. A halmokat hidraulikusan leválasztották a csatornaágyról (balra a 2a. Ábra). Ez a rendszer megfelel a Bouwer [2002]. Fiatalok [1977] homogén víztartót vett át nem ereszthető fenékkel, és egy eltömődött árok alatti halom átmeneti problémáját tanulmányozta. KB egy szubsztrátummal ellátott kétrétegű képződményt vizsgált, bár szoros, de véges vezetőképességű.

Phreatic felületek B1C1 és B2CA 2. réteg a felső rétegben egy telített zónát határol a MAR-tolla oldalirányú terjedéséről. Az 1. ábra második rétegének kapillaritása is kicsi, ezért könnyen kimutatható, hogy egy átmeneti Green-Ampt (GA) modell (lásd: PK) elülső „beszivárgás”, f (t), a határfelületről az ősi hordalékba terjedve, megjósolja az ilyen állandó állapotú „beszivárgás” gyors kialakulását. Ezt az elülső és majdnem függőleges petyhüdt freatikus felületeket (három szaggatott pontozott görbe az 1. ábra második rétegében) az állandó állapotú szivárgás váltja ki (emlékeztetünk rá, hogy néhány hétig-hónapig tart) a csatornából. A x a felső réteg hidraulikus fejének felülete az interfész szegmens felett C2ACAz 1. ábrán az ebből a rétegből a szubsztrátumba való folyamatos beszivárgás sebessége állandó és egyenlő k2. Ez az alapfeltevés KBmodellje és a klasszikus GA infiltrációs modell, PK, a beszivárgás „késői fázisához”.

Fő célunk a csatornából származó áramlási sebesség meghatározása, 2Q. Ez egy kulcs MAR paraméter. Ha nincs impedancia a második rétegtől, vagyis ha b = ∞ (vagy k2 = k1) az 1. ábrán, majd Q = k1c. Az alacsonyan áteresztő réteg csökken Q. Ha k2 = A 0. ábrán látható, hogy az 1. ábrán látható csatornától nem triviális egyenletes szivárgás vízszintes, át nem eresztő síkon, valamint bármely más áramlás lehetséges Bouwer-rendszerben sem. Matematikailag ez azt jelenti, hogy a freatikus felületek nagy időn belül felemelkednek, végül egybeesnek a 2a. Ábra abszcisszatengelyével és az áramlás leáll.

A közelmúltban felmerült az érdeklődés a víztartó réteg egyik állapotának a másikba való átmenetének jellegzetes időpontjai iránt, különféle természetes és ember által létrehozott hidrológiai hajtások alatt [lásd pl., Currell és mtsai., 2015; Simpson és mtsai., 2013]. A 2. ábrán látható eltömődött csatornától az állandó állapot eléréséhez szükséges átlagos cselekvési idő nyelvén végtelen, és megfelel az álló talajvíznek, amely teljesen lefedi az egész talajréteget, hasonlóan a Fiatalok [1977] árokból áramlik. A gyakorlatban ezt a nyugalmi talajvízállapotot soha nem érik el, mert ha a MAR folyamatos, az utántöltött víz mindig megtalálja szellőzőnyílásait a víztartóból: párolgás, transzpiráció, topográfiai mélyedéseken keresztüli kifolyások, az alapkőzet enyhe lejtőjén lefelé sodródás (ami soha nem ideális vízszintes, mint Hantush vagy Youngs MAR-sémáiban) és az óceánba történő lefolyás vagy a halomból történő pumpálás.

Érdeklõdésünk második jellemzõje az 1. ábrán látható gyulladásos felületek alakja. Bár az ománi MAR szakaszos, nemrégiben azt figyelték meg, hogy az 1. ábra legutóbbi hordalékának váratlan vízhozamai messze elterjednek a MAR forrásoktól, különösen a városi területeken ahol a párolgás és a mezőgazdasági szivattyúzás minimális, és az alapok károsodása jelentős. Ha a MAR-vizet nyáron kívánják visszanyerni (a muskotályi dísznövények öntözésének nagy igénye), a szivattyúkutak és szitáik helyének jól illeszkednie kell a telített áramlási tartományhoz, Gz,Figyelembe véve, hogy az 1. ábrán látható csak „ideiglenes állandó állapot”, az 1. ábra talajvíz halmának tervezett helyreállításakor fel kell ismerni, hogy az 1a. ábra második rétegéből történő szivattyúzás sokkal nehezebb. és drága, mint a felső rétegből, és a repedezett kőzetből történő kinyerés (az 1. ábra harmadik rétege) gyakran műszakilag lehetetlen.

2 Matematikai modell és analitikai megoldás

Bevezetjük a derékszögű koordinátákat, xOy, eredettel O egybeesik a csatorna középpontjával. Összetett fizikai síkon z = x + iy, az áramlási tartomány szimmetrikus a Oy tengelyt, és ennek a tartománynak a jobb felében vizsgáljuk az áramlást, Gz. A hidraulikus fej h(x, y) harmonikus függvény Gz. Bevezetünk egy komplex w = ϕ + i ψ potenciált, ahol ϕ = - k 1 h a sebességpotenciál és ψ egy áramfüggvény. A darciai sebesség, V → (x, y), engedelmeskedik a V → (x, y) = - k ∇ h értéknek. Összetett darciai sebesség V = u + iv van meghatározva, ahol u(x, y) és v(x, y) a sebességvektor vízszintes és függőleges komponensei. A komplex funkció V(z) antiholomorf (PK) és w(z) holomorf.

Attól számoljuk a fejét B1O ahol ϕ = 0 és az adatfolyam függvény - innen OA, amely mentén ψ = 0. A KB modell feltételezi v = −k2 mentén AC1 és ezért ψ = k 2 x ezen a határ mentén. A freatikus felület mentén a nyomás atmoszférikus (a kapillaritást elhanyagoljuk), ezért along + k 1 y = 0 B1C1. Ez a szabad határ egyben áramvonal ψ = Q. Pontban CAz 1. ábrán, amelynek helye a megoldás része, a szabad felület metszi a két réteg közötti határfelületet, és ezért ψ C 1 = Q = k 2 L. A hodográf tartomány, GV, megfelelő Gz, ábra a 2b. ábrán látható. Ebben a tartományban, B1CAz 1. kör sugara körív k1/2.

A komplex potenciális tartomány Gw a 2c. ábra mutatja. Itt a kép ACAz 1. egy ismeretlen görbe, ezért Gw egy görbe vonalú téglalap. Val vel GV egy kör alakú háromszöget, akkor a PK módszer a megadott határérték-probléma (BVP) leképezéssel történő megoldására GV egy kiegészítő félsíkra az 1d. ábra úgy, hogy az O pont képe az legyen −p ebben a síkban. (lásd az A. függeléket). Felidézzük, hogy matematikailag a módszer a Riemann-probléma megoldására épül [Gakhov, 1966].

Dimenzió nélküli változókat vezetünk be (z *, b *, w *, k *, L *, Q *, S *) = (z/c, b/c, w/(k1c), k2/ k1, L/c, Q/(ck1), S/c 2 ) és a rövidség kedvéért dobja el a feliratokat. Példaként két esetet számoltunk ki egy sekély és egy mély felső rétegről: b = 1.0 és b = 3,0 (3., illetve 4. ábra). A vízszint jobb ágai a csatorna szélétől indulnak x = 1, y = 0.

A freatikus felület jobb ágai a csatorna szélétől a szivárgó aljzatig terjednek b = 1 (folytonos vonalak) és a Borz aszimptotikus vízszint (szaggatott vonal).