Stabilitási fizika

A szakasz végére:

Mondja el az egyensúly típusait.
Ismertesse a stabil és instabil egyensúlyokat!.
Írja le a semleges egyensúlyt.

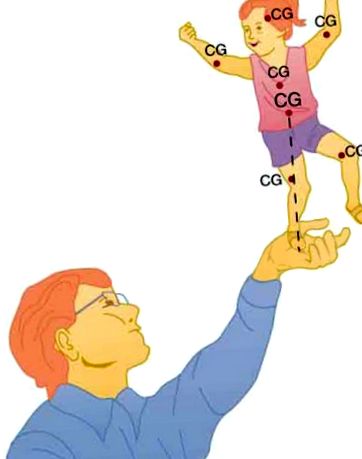
Egy dolog, ha egy rendszer egyensúlyban van; egészen más, hogy stabil legyen. Az 1. ábrán a férfi kezére ülő játékbaba nincs stabil egyensúlyban. Az egyensúlynak három típusa van: stabil, instabil és semleges. A modul ábrái különféle példákat mutatnak be.

Az 1. ábra egy kiegyensúlyozott rendszert mutat be, például az ember kezén lévő játékbabát, amelynek a súlypontja (cg) közvetlenül a forgócsap felett helyezkedik el, így az össztömeg nyomatéka nulla. Ez egyenértékű azzal, hogy az egyes alkatrészek nyomatékai ki vannak egyensúlyozva az elfordulási pont körül, ebben az esetben a kéz. A karok, a lábak, a fej és a törzs cg-je kisebb típussal van ellátva.

1. ábra: Egy férfi egy játékbabát egyensúlyoz.

Azt mondják, hogy egy rendszer stabil egyensúlyban van, ha az egyensúlyból elmozdulva nettó erőt vagy forgatónyomatékot tapasztal az elmozdulás irányával ellentétes irányban. Például egy tál alján lévő márvány helyreállító erőt fog tapasztalni, ha elmozdul az egyensúlyi helyzetéből. Ez az erő visszahelyezi az egyensúlyi helyzet felé. A legtöbb rendszer stabil egyensúlyban van, különösen kis elmozdulások esetén. A stabil egyensúly egy másik példáját lásd a 2. ábrán látható ceruzában.

2. ábra: Ez a ceruza egyensúlyi állapotban van. A ceruzán a nettó erő nulla, a forgatócsapok teljes nyomatéka pedig nulla.

Egy rendszer instabil egyensúlyban van, ha elmozduláskor nettó erőt vagy forgatónyomatékot tapasztal ugyanabban az irányban, mint az egyensúlyból való elmozdulás. Az instabil egyensúlyi rendszer felgyorsul egyensúlyi helyzetétől, ha kissé elmozdul. Nyilvánvaló példa erre a domb tetején pihenő labda. Miután elmozdult, felgyorsul a címertől. Az instabil egyensúly példáit lásd a következő néhány ábrán.

3. ábra: Ha a ceruzát kissé oldalra toljuk (az óramutató járásával ellentétes irányba), akkor már nincs egyensúlyban. Súlya az óramutató járásával megegyező irányú forgatónyomatékot eredményez, amely visszaállítja a ceruza egyensúlyi helyzetét.

4. ábra: Ha a ceruzát túlságosan elmozdítják, a súlya által okozott nyomaték az óramutató járásával ellentétes irányba változik, és növeli az elmozdulást.

5. ábra: Ez az ábra instabil egyensúlyt mutat, bár az egyensúly mindkét feltétele teljesül.

6. ábra: Ha a ceruzát kissé elmozdítják, akkor a súlya egy olyan nyomatékot hoz létre, amely ugyanabban az irányban van, mint az elmozdulás, ami az elmozdulás növekedését okozza.

Egy rendszer semleges egyensúlyban van, ha egyensúlya független az elmozdulástól az eredeti helyzetétől. Példa erre a márvány sík vízszintes felületen. Ezeknek a helyzeteknek a kombinációja lehetséges. Például a márvány a nyeregben stabil a nyereg elülső vagy hátsó része felé történő elmozdulásokhoz, és instabil az oldalsó elmozdulásokhoz. A 6. ábra a semleges egyensúly egy másik példáját mutatja be.

7. ábra (a) itt a semleges egyensúlyt látjuk. A sík felületen lévő gömb cg-je közvetlenül a támaszpont felett helyezkedik el, függetlenül a felület helyzetétől. A gömb tehát bármely helyen egyensúlyban van, és ha elmozdul, akkor helyben marad. (b) Mivel kör keresztmetszetű, a ceruza semleges egyensúlyban van a hosszára merőleges elmozdulásokhoz.

Ha azt vesszük figyelembe, hogy egy stabil egyensúlyban lévő rendszer milyen mértékben képes elmozdulni, mielőtt instabillá válna, azt találjuk, hogy egyes stabil egyensúlyban lévő rendszerek stabilabbak, mint mások. A 2. ábrán látható ceruza és a 8. (a) ábra szerinti személy stabil egyensúlyban van, de instabillá válnak viszonylag kis oldalirányú elmozdulások esetén. A kritikus pont akkor érhető el, amikor a cg már nem lépi túl a támasz alapját. Ezenkívül, mivel egy személy testének cg-je a csípő forgáspontjai felett van, az elmozdulásokat gyorsan ellenőrizni kell. Ez a kontroll egy központi idegrendszeri funkció, amely akkor alakul ki, amikor megtanuljuk testünket csecsemőként felállítani. A nagyobb stabilitás érdekében a lábakat szét kell szétteríteni, nagyobb támasztékot biztosítva. A stabilitás azáltal is növekszik, hogy a térd hajlításával csökkenti az ember súlypontját, például amikor egy futballista felkészül arra, hogy labdát kapjon, vagy egy merevítőt rögzít egy felszereléshez. A vessző, a mankó vagy a járóka növeli a felhasználó stabilitását, még jobban, amikor a támasz alapja kiszélesedik. Általában a nőstény cg-je alacsonyabb (közelebb a talajhoz), mint egy hím. A kisgyermekek súlypontja a válluk között van, ami növeli a járás megtanulásának kihívását.

8. ábra (a) egy felnőtt súlypontja a csípőízületek felett (a test egyik fő csuklója) helyezkedik el, és két keskenyen elkülönített láb között helyezkedik el. Mint a radírján álló ceruza, ez a személy is stabil egyensúlyban van az oldalirányú elmozdulásokkal szemben, de a viszonylag kis elmozdulások a cg-t a tartó alján kívülre viszik és instabillá teszik. Az emberek kevésbé stabilak az előre és hátra történő elmozdulásokhoz képest, mert a lábak nem túl hosszúak. Az izmokat széles körben használják a test ki-egyensúlyozásához elöl-hátul. b) A hajlítás a bemutatott módon történõ megnövelése esetén a stabilitás a súlypont csökkentésével növekszik. A stabilitás akkor is növekszik, ha az alapot úgy tágítják, hogy a lábakat egymástól távolabb helyezzük el.

Az olyan állatok, mint a csirkék, könnyebben kezelhetőek. A 9. ábra azt mutatja, hogy egy csirke cg-je a csípőízületei alatt, valamint a szélesen elválasztott és széles lábak között fekszik. Még a csirke cg-jének viszonylag nagy elmozdulása is stabil, és olyan erőket és forgatónyomatékokat eredményez, amelyek a csirkét csekély erőfeszítéssel visszaállítják egyensúlyi helyzetébe. Természetesen nem minden madár olyan, mint a csirkék. Néhány madár, például a flamingó egyensúlyi rendszere szinte ugyanolyan kifinomult, mint az embereké.

A 9. ábra azt mutatja, hogy egy csirke cg-je a csípőízületek alatt van, és egy széles támaszpont felett helyezkedik el, amelyet széles körben elválasztott és nagy lábak alkotnak. Ezért a csirke nagyon stabil egyensúlyban van, mivel az instabillá válásához viszonylag nagy elmozdulás szükséges. A csirke testét felülről támasztja alá a csípő, és a csípők között ingaként működik. Ezért a csirke stabil az első-hátsó elmozdulások, valamint az oldalról a másikra történő elmozdulások esetén.

9. ábra: A csirke súlypontja a csípőízületek alatt található. A csirke stabil egyensúlyban van. A csirke testét felülről támasztja alá a csípő, és ingaként működik közöttük.

A mérnökök és az építészek arra törekszenek, hogy rendkívül stabil egyensúlyokat érjenek el az épületek és egyéb rendszerek számára, amelyeknek ellen kell állniuk a szélnek, a földrengéseknek és más erőknek, amelyek kiszorítják őket az egyensúlyból. Bár ebben a szakaszban a példák a gravitációs erőket hangsúlyozzák, az egyensúly alapvető feltételei minden erőtípus esetében azonosak. A nettó külső erőnek nullának kell lennie, és a nettó nyomatéknak is nullának kell lennie.

Hazavihető kísérlet

Álljon egyenesen a sarkával, hátával és fejével a falnak. Hajoljon előre a derekától, a sarkát és az alját a falhoz tartva érintse meg a lábujjait. Meg tudja csinálni ezt anélkül, hogy felborulna? Magyarázza el, miért és mit kell tennie ahhoz, hogy egyensúlyának elvesztése nélkül megérinthesse a lábujjait. Könnyebb ezt egy nőnek megtenni?

Szakasz összefoglaló

Azt mondják, hogy egy rendszer stabil egyensúlyban van, ha az egyensúlyból elmozdulva nettó erőt vagy forgatónyomatékot tapasztal az elmozdulás irányával ellentétes irányban.
Egy rendszer instabil egyensúlyban van, ha az egyensúlyból elmozdulva nettó erőt vagy forgatónyomatékot tapasztal ugyanabba az irányba, mint az egyensúlyból való elmozdulást.
Egy rendszer semleges egyensúlyban van, ha egyensúlya független az elmozdulástól az eredeti helyzetétől.

Fogalmi kérdések

1. Az oldalán fekvő kerek ceruza a 4. ábra szerint semleges egyensúlyban van a hosszára merőleges elmozdulásokhoz képest. Mi a stabilitása a hosszával párhuzamos elmozdulásokhoz képest?

2. Magyarázza meg a függőleges hídon lévő magas tornyok szükségességét a stabil egyensúly biztosítása érdekében.

Problémák és gyakorlatok

1. Tegyük fel, hogy a ló a falnak támaszkodik, ahogy a 10. ábra mutatja. Számítsa ki a falra kifejtett erõt feltételezve, hogy az erõ vízszintes, miközben felhasználja az adatokat a helyzet sematikus ábrázolásában. Ne feledje, hogy a falra kifejtett erő nagysága megegyezik és iránya ellentétes a lóra kifejtett erővel, egyensúlyban tartva azt. A ló és a lovas össztömege 500 kg. Vegyük az adatokat három számjeggyel pontosabbá.

2. Két 20 kg és 30 kg tömegű gyermek kiegyensúlyozottan ül egy libikócán, és a forgáspontja a hinta közepén helyezkedik el. Ha a gyerekeket 3 m távolság választja el egymástól, akkor az elfordulási ponttól milyen távolságban ül a kisgyerek az egyensúly fenntartása érdekében?

3. a) Számítsa ki a 10. ábrán a ló mindkét lábára ható erő nagyságát és irányát (kettő a földön van), feltételezve, hogy a ló tömegközépe a lábak közepén van. A ló és a lovas teljes tömege 500 kg. b) Mi a minimális súrlódási együttható a paták és a talaj között? Vegye figyelembe, hogy a fal által kifejtett erő vízszintes.

4. Egy személy 2 m hosszú deszkát hordoz, egyik kezével F1 erővel lenyomva az egyik végén, a másik kezével pedig F2 erővel 50 cm-re feltartva a deszka végétől. Ha a deszka tömege 20 kg, és a súlypontja a deszka közepén van, akkor mekkora az F1 és F2 erő?

5. Egy 17,0 m magas és 11,0 m hosszú építés alatt álló falat és annak merevítését a 11. ábra mutatja. A fal stabil egyensúlyban van a merevítés nélkül, de az alján elfordulhat. Számítsa ki a 10 merevítő erejét, ha az erős szél 650 N vízszintes erőt fejt ki a fal négyzetméterére. Tegyük fel, hogy a szél által okozott nettó erő a fal félig felfelé eső magasságban hat, és hogy minden merevítő egyenlő erőket fejt ki hosszával párhuzamosan. Hanyagolja el a fal vastagságát.

6. a) Milyen erőt kell kifejtenie a szélnek, hogy egy 2,50 kg-os csirkét a 12. ábrán látható helyzetben támogasson? b) Mennyi az erő és a csirke súlya? (c) Ez alátámasztja-e azt az állítást, hogy a csirke szerkezete viszonylag stabil?

7. Tegyük fel, hogy a 12. ábrán látható felvonóhíd súlyát teljes egészében a csuklópántjai és a szemközti part támasztja alá, hogy kábelei lazák legyenek. a) A tömeg mekkora részét támasztja alá a szemközti part, ha a támasztási pont közvetlenül a kábelrögzítők alatt van? (b) Milyen irányban és nagyságrendű erővel bír a zsanérok a hídon ilyen körülmények között? A híd tömege 2500 kg.

13. ábra: Egy kis felvonóhíd, amely a csuklópántokon (F), a súlyán (w) és a huzalok feszültségén (T) látható.

8. Tegyük fel, hogy egy 900 kg-os autó van a 13. ábrán látható hídon, tömegközépe félig a zsanérok és a kábelrögzítők között. (A hidat csak a kábelek és a zsanérok támasztják alá.) (A) Keresse meg az erőt a kábelekben. (b) Keresse meg a híd zsanérjai által kifejtett erő irányát és nagyságát.

9. A szendvicspanel reklámtáblája a 14. ábrán látható módon készül. A tábla tömege 8,00 kg. (a) Számítsa ki a lánc feszültségét, feltételezve, hogy nincs súrlódás a lábak és a járda között. b) Milyen erőt fejt ki mindkét oldal a csuklóra?

14. ábra: A szendvicspanel reklámtáblája feszültséget mutat.

10. a) Milyen minimális súrlódási együtthatóra van szükség a lábak és a talaj között, hogy a 14. ábrán látható jel a mutatott helyzetben maradjon, ha a lánc megszakad? b) Milyen erőt fejt ki mindkét oldal a csuklóra?

11. A tornász megpróbálja hasításokat végrehajtani. A 15. ábrán megadott információk alapján számítsa ki a lábak által a padló által kifejtett erő nagyságát és irányát.

15. ábra A tornász teljes osztást végez. Megjelenik a súlypont és a különféle távolságok.

Szójegyzék

A problémák és válaszok kiválasztott megoldásai

1. Fall = 1,43 × 10 3 N

3. a) 2,55 × 10 3 N, 16,3 ° a függőlegestől balra (azaz a fal felé) b) 0,292

7. a) 0,167, vagyis a súly körülbelül egyhatodát az ellenkező part támasztja alá. (b) F = 2,0 × 10 4 N, egyenesen felfelé.