Kapilláris kering

Tárgyak

Absztrakt

A folyadék felületén rekedt milliméter méretű tárgyak súlyukkal torzítják az interfészt, ami viszont egymás felé vonzza őket. Ez a mindenütt jelenlévő jelenség, amelyet köznyelven „Cheerios-effektusnak” neveznek, a gabonafélék reggelizőtálba való összecsomósodásában jelentkezik, és nagyon ígéretes útnak bizonyul a kolloid részecskék ellenőrzött önfelszaporodása felé a víz felszínén. Itt kapilláris vonzódást vizsgálunk a lebegő cseppek között, amelyek a folyékony nitrogén felett fordított Leidenfrost állapotban vannak fenntartva. Kiderül, hogy a cseppek spontán keringenek egymás körül - tükrözve egy miniatűr égi rendszert. Ebben az elhanyagolható súrlódási helyzetben a pályákat kizárólag a Cheerios-interakciós potenciál alakítja, amelyet közvetlenül a csepp dinamikájából nyerünk. Eredményeink eredeti perspektívát kínálnak az érintésmentes és szennyezésmentes cseppek krioprezerválásának feldolgozásáról, ahol a Leidenfrost-hatást és a kapillaritást szinergiában alkalmaznák a biológiai minták üvegesítésére és szállítására.

Bevezetés

Itt a húzás megkerülésével tovább toljuk az összehasonlítást: megmutatjuk, hogy a kapilláris vonzásnak alávetett lebegő részecskék sokféle bonyolult pályát követnek. A Cheerios interakciós potenciál által kialakított pályák alapvetően különböznek a szokásos newtoni kúpoktól. A súrlódás hiányát kihasználva közvetlenül levezetjük a Cheerios interakciós potenciált a részecske dinamikájából, és modellezzük a kísérleti pályákat. Végül megvitatjuk a korlátozott pályák megszerzésének lehetőségét.

Eredmények

Súrlódásmentes cseppek pályája

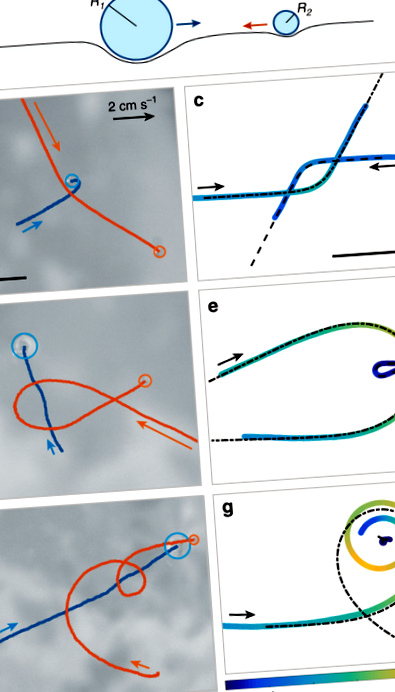
Két szilikonolajcsepp mozgását figyeljük meg (sugarakkal R1 és R2, 250 μm és 1,4 mm között) óvatosan szabadon engedjük a folyékony nitrogén nyugvó fürdője felett. Amint azt az 1a. Ábra szemlélteti, minden cseppet „inverz Leidenfrost” állapotban tartunk a folyadék felszíne felett, amely lebegő állapotot a 16, 17, 18, 19 kriogén fürdő által létrehozott folyamatos gőzáram lehetővé teszi. Ennek a rendszernek egyedülálló tulajdonsága, hogy a fürdővel való fizikai érintkezés hiányában a súrlódási erők rendkívül kicsiek maradnak (20,21,22), és a gyors mozgás hasonlít a Leidenfrost szokásos cseppjeihez, amelyek nagyon mozgékonyak, ha külső mezőkbe kerülnek 23. Ezenkívül kísérletünkben ezt a kis ellenállást szinte tökéletesen kompenzálja a kicsi meghajtó erő, amelyet a film cseppjeit fenntartó filmben lévő szimmetria törése okoz. A cseppek így szinte súrlódásmentes „kriogén korcsolyázóként” viselkednek: tökéletesen egyenes pályákon siklanak, és miután megdermedtek, állandó sebességet tartanak v0 1 és 3 cm közötti s -1. A lebegés és a meghajtás a cseppek lehűlésével fennmarad, és csak kapilláris kölcsönhatásnak kitett fagyott márványokat eredményez.

Interakciós potenciál

Érdekes módon kísérletünkben a súrlódás hiánya a kapilláris interakciós potenciál közvetlen mérését kínálja E. Nicolson-féle közelítésben, ahol a deformációk kicsiek, két nem nedvesítő objektum (180 ° -os érintkezési szöggel) interakciós potenciálja egymástól r és tömegekkel m1 és m2 a 3-at olvassa

amely a pontrészecskék közötti kölcsönhatásként is felfogható 24. Ebben a kifejezésben g a gravitációt jelenti, és γ, ρ, és ρN a részecske és a fürdő felületi feszültsége, illetve sűrűsége. A \ (K_0 (r> a) \) függvény a zeroth-sorrendben módosított második fajta Bessel-függvény, és tükrözi az interfész által a m1, amelyet érez m2 (és fordítva). A hosszméret \ (a = \ sqrt \) a fürdő kapilláris hossza. A \ (r \, távolságokon a \ (K_0 (r/a) \) függvény logaritmikusan eltér a kétdimenziós newtoni gravitációval és az elektrosztatikával analóg módon. \ (R \,> \, a \) esetében azonban a kölcsönhatások exponenciálisan bomlik. A képlet kísérleti igazolásához két csepp tömegű rendszert veszünk figyelembe m1 és m2 egymás felé haladva. A kéttestes rendszert átformáljuk csökkentett tömegű egytest problémává \ (m_r = \ frac >> \). Szétszóródás hiányában a kapilláris potenciál E(r) ekkor közvetlenül a kinetikus energiából következtethetünk Ek a redukált részecske felhasználásával \ (E (r) = E_k - E_k \ bal (\ jobb) \) .

A 2. ábrán négy frontális ütközést és két kis eltérést választottunk ki, és ábrázoltuk a dimenzió nélküli kapillárispotenciált \ (E (r)/(m_1m_2C) \), amint arra a részecske dinamikájából következtethetünk. Minden kísérlet más színnel van ábrázolva, amint azt a betétlap mutatja. A részecske sugara szisztematikusan 290 μm és 1,4 mm között változik. Minden kísérleti adat egyetlen görbére omlik össze, kiváló összhangban az elméleti előrejelzéssel \ (K_0 (r/a) \), állítható paraméterek nélkül, bizonyítva, hogy az interakciós potenciál (1) távoli kifejezése még mindig fennáll, ha a cseppek elég közel vannak az ütközéshez. A kis deformáció kritériuma valóban érvényes a legnagyobb cseppekre is, amelyek csak távolságban képesek kölcsönhatásba lépni r > R1 + R2. Ezen viszonylag nagy távolságoknál a fürdő deformációja mindig kisebb, mint 100 μm.

A Cheerios-potenciál kísérleti mérése. A kísérleti (nem dimenziós) potenciált \ (E (r)/(Cm_1m_2) \) egy részecskepár dinamikájából vonják ki. Mindegyik szín egy másik kísérletnek felel meg, a részecskék sugara és tömegaránya szisztematikusan változik. A kísérleti adatokat összehasonlítjuk a potenciál elméleti alakjával \ (K_0 (r/a) \), fekete vonallal ábrázolva

Kapilláris kering

A kifejezéssel E(r) a kezében az Eq. (1) az 1. ábrán bemutatott részecske-pályák kiszámításához. A gravitációhoz hasonlóan a potenciál is arányos a két tömeg szorzatával, de más módon függ a részecske távolságától. Itt szisztematikusan feltárjuk, hogyan befolyásolják a jól ismert égi pályákat az 1 /r-ebben a szokatlan, Bessel-alakú forma által rejlő potenciál \ (K_0 (r/a) \) .

Tesztként először numerikusan integráljuk a mozgásegyenleteket, az 1. ábra kísérleteinek megfelelő kezdeti feltételeket felhasználva. A kezdeti sebességet (amelyet a kísérleti adatok zajával kompatibilis értékeken belül veszünk) választjuk meg a legjobb illeszkedés érdekében, a négyzet alapértelmezett hibaminimalizálásával. A kapott pályákat szaggatott vonalakkal helyezzük el, és közvetlenül összehasonlítjuk a kísérletekkel. Az így kapott jóslatok szinte tökéletesen illeszkednek az 1c. Ábra kísérleti pályáihoz, pl. Az 1g. Ábra dinamikáját azonban nem sikerül megismételni: a számított pálya nagy elhajlást jósol ütközés nélkül. Általánosabban kiderül, hogy a modell pontosan leírja kísérleteink többségét kis elhajlásokra és ütközésekre, miközben szisztematikusan alábecsüli az elhajlás amplitúdóját, ha a részecskék több mint 270 ° -kal térnek le. Amint az alábbiakban tárgyaljuk, ezt egy kis, de nem elhanyagolható súrlódási energiaveszteségnek tulajdonítjuk, amely akkor következik be, amikor a cseppek jelentős sebességváltozásokat tapasztalnak.

A kapilláris pályák szisztematikus osztályozását (súrlódás nélkül) a központi erőterek standard megközelítését követve kapjuk meg 25. Bemutatjuk a hatékony kapilláris potenciált Ua kapcsolódó részecske effektje csökkentett tömeggel mr

a pálya szögmomentumának elszámolása \ (L = m_rr ^ 2 \ dot \ theta \) .

A 3a. Ábra mutatja Ueff változóval L, a tipikus kísérleti körülményekhez (lásd a feliratot). A skála nélküli algebrai potenciálokkal szemben, UAz effektum minimálisan csak elég kicsi L, amely a választott paraméterekhez (csökkentett tömeg \ (m_r = 9.10 ^< - 8>\) kg, és a kezdeti távolság r0 = 4,1 mm) megfelel a kezdeti szögsebességnek \ (\ dot \ theta _0 \, rad s −1. Ez a korlátozás a kapilláris hosszon túli interakció szűrésének közvetlen következménye a. Korlátozott pályák lehetségesek, ha van egy minimum, amire a 3b. Ábra (és a 7. kiegészítő film) példát mutat be. A határolt államok virágszerű mintákat mutatnak be, nem pedig zárt pályákat, amelyek Bertrand 26, 27-es tétele szerint a −1 /r és r 2 potenciál. Ennek a hatásnak a legfontosabb példáját a higany perihéliumának precessziója adja, az 1/1 relativisztikus korrekciói miatt.r lehetséges. A 3b. Ábra példájában a precessziós szög 109 °.

A kapilláris pályák osztályozása. a Hatékony potenciál Ueff a távolság függvényében r, a kezdeti szögsebesség változtatásához \ (\ dot \ theta _0 \). A részecske tömegét és kezdeti távolságát állandó értéken tartjuk (\ (m_r = 9.10 ^< - 8>\) kg, és r0 = 4,1 mm). b Példa erre a potenciálra korlátozott pályára, kezdeti feltételekkel \ (\ dot \ theta _0 \) = 1,465 rad s −1 és \ (\ dot r_0 \) = 0. Lásd még a 7. kiegészítő filmet. c Fázisdiagram a pályák osztályozásához, a kezdeti feltételek felhasználásával kifejezve r0, \ (\ dot \ theta _0 \) \ (m_r = 9,10 ^)< - 8>\) kg. A felső régió az elhajlásoknak, az alsó régió pedig az ütközéseknek felel meg, mindkettőt kísérleti pályák szemléltetik. Az ütközés nélküli kötött pályák csak egy keskeny sávban figyelhetők meg, szürke árnyalatokkal ábrázolva, változó sugársebesség esetén \ (\ dot r_0 \). A (d) piros kereszt jelzi. d Kísérleti pálya korlátozott pályához közel a tömegkeret közepén. Lásd még a 8. kiegészítő filmet

Vita

Az energiaveszteség hatása. a Két sugárral rendelkező részecske kísérleti pályája R1 = 360 μm és R2 = 340 μm. Lásd még a 9. kiegészítő filmet. b Kétcseppes rendszer energiavesztesége ((Delta E _ >> \) az idő függvényében (kék színnel). A modellezett ΔE szaggatott vonallal van ábrázolva. c A két részecske pályája a tömegkeret közepén, sebességüknek két különböző színkóddal. A szaggatott vonalak a modellezett pályák, amelyeket numerikusan számolunk, integrálva (az egyes részecskékre) egy kis súrlódási erőt, amelynek nagysága \ (F = \ frac> \ bal (\ jobb) \) és a részecske sebességével ellentétes irányú V

Eredményeink feltárják a súrlódásmentes részecskék képességét érzékeny szondákként történő működésre, amelyek felhasználhatók a kapilláris önszerelést irányító erők közvetlen mérésére. A jelenlegi vizsgálatban bemutatott kapillaritás ellenőrzése kiemelkedő jelentőségű az egyre növekvő alkalmazásokban, például a csepp krioprezerválásban 28,29,30: a kriogén levitáció egyedülálló módszert kínál a cseppek gyors üvegesítésére 16,18, minimális szennyeződés veszélyével, ugyanakkor idő, amely rendkívül sokoldalú eljárást kínál az ilyen biológiai minták távoli kiválasztására, kezelésére és rendszerezésére az optimális kezelés és megőrzés érdekében.

Mód

kísérleti eljárás

Szilikonolaj cseppek (sűrűséggel ρ = 930 kg m - 3 és viszkozitás η = 9,3 mPa s) néhány centiméterrel szabaddá válnak a még folyékony nitrogénfürdő felülete felett. Nagy cseppek (sugárral R > 750 μm) kalibrált Hamilton tűk felhasználásával keletkeznek, míg kisebbek (250 μm 17,19. Az áldozati fürdő átmérője 19 cm, 5 cm folyékony nitrogénnel van feltöltve. Az áldozati fürdő forralása nitrogén atmoszférát eredményez. és részben szigeteli a központi fürdőt, amely mozdulatlanul tartja a felületet. Mindkét főzőpoharat házi készítésű polisztirol kriosztátba helyezzük, belső méretű 20 × 20 × 15 cm 3 és 4 cm vastag falakkal. A kísérleteket felülről filmezzük, jellemzően 500 kép/mp sebességgel. nagysebességű kamera (Photron Mini UX-100) segítségével. A doboz fedelét minden kísérletnél (amely általában 1 percig tart) eltávolítják, majd visszahelyezik a szigetelés biztosítására. A csepp pályákat végül házi Python algoritmus segítségével követik nyomon.

Az adatok elérhetősége

A tanulmányt alátámasztó adatok a megfelelő szerző kérésére rendelkezésre állnak.

Hivatkozások

Nicolson, M. M. Az úszó részecskék közötti kölcsönhatás. Math. Proc. Camb. Philos. Soc. 45, 288–295 (1949).

Chan, D., Henry, J. Jr. és White, L. R. A folyadékfelületeken összegyűjtött kolloid részecskék kölcsönhatása. J. Colloid Interface Sci. 79, 410–418 (1981).

Vella, D. & Mahadevan, L. A „cheerios-effektus”. Am. J. Phys. 73., 817–825 (2005).

Gart, S., Vella, D. & Jung, S. A fonálférgek kollektív mozgása vékony folyékony rétegben. Lágy anyag 7, 2444–2448 (2011).

Loudet, J. & Pouligny, B. Hogyan gyülekeznek a szúnyogtojások a víz felszínén? Eur. Phys. J. E 34, 76 (2011).

Singh, P., Joseph, D. és Aubry, N. A folyadék-folyadék felületeken úszó részecskék diszperziója és vonzása. Lágy anyag 6., 4310–4325 (2010).

Dalbe, M. J., Cosic, D., Berhanu, M. & Kudrolli, A. A súrlódó részecskék összesülése a kapilláris vonzerő miatt. Phys. Jel. E 83., 051403 (2011).

Bleibel, J., Domnguez, A., Oettel, M. & Dietrich, S. kolloidok kollektív dinamikája folyadékinterfészeken. Eur. Phys. J. E 34, 125 (2011).

Whitesides, G. M. és Grzybowski, B. Öngyülekezés minden léptékben. Tudomány 295, 2418–2421 (2002).

Snezhko, A. & Aranson, I. S. Saját összeszerelésű kolloidális őszirózsák mágneses manipulálása. Nat. Mater. 10., 698 (2011).

Botto, L., Lewandowski, E., Cavallaro, M. & Stebe, K. kapilláris kölcsönhatások anizotrop részecskék között. Lágy anyag 8., 9957–9971 (2012).

Ershov, D., Sprakel, J., Appel, J., Stuart, M. & van der Gucht, J. A gömbös kolloidok kapillaritás által kiváltott rendezése anizotrop görbületű interfészen. Proc. Natl Acad. Sci. USA 110, 9220–9224 (2013).

Hu, D. és Bush, J. meniszkuszra mászó rovarok. Természet 437, 733 (2005).

Peruzzo, P., Defina, A., Nepf, H. M. és Stocker, R. úszó részecskék kapilláris lehallgatása felszúró növényzet által. Phys. Tiszteletes Lett. 111., 164501 (2013).

Bleibel, J., Dietrich, S., Domínguez, A. & Oettel, M. sokkhullámok a kolloidok kapilláris összeomlásában: modellrendszer kétdimenziós átvilágított newtoni gravitációhoz. Phys. Tiszteletes Lett. 107., 128302 (2011).

Song, Y. S. és mtsai. Folyékony cseppek üvegesítése és levitálása folyékony nitrogénen. Proc. Natl Acad. Sci. USA 107., 4596–4600 (2010).

Adda-Bedia, M. és mtsai. Fordított leidenfrost-hatás: levitáló cseppek a folyékony nitrogénre. Langmuir 32, 4179–4188 (2016).

Feng, H., Xu, Y. és Yang, T. tanulmány a krioprotektáló cseppek leidenfrost-hatásáról folyékony nitrogénre IR képalkotó technológiával és nem izoterm kristályosodási kinetikai modellel. Int. J. Heat. Mass Transf. 127., 413–421 (2018).

Gauthier, A., Diddens, C., Proville, R., Lohse, D. & van der Meer, D. Az inverz leidenfrost cseppek önmeghajtása kriogén fürdőn. Proc. Natl Acad. Sci. USA 116, 1174–1179 (2019).

Biance, A.-L., Clanet, C. & Quéré, D. Leidenfrost cseppek. Phys. Folyadékok 15, 1632–1637 (2003).

Le Merrer, M., Clanet, C., Quéré, D., Raphaël, É. & Chevy, F. hullám húzza az úszó testeket. Proc. Natl Acad. Sci. USA 108., 15064–15068 (2011).

Hale, J. & Akers, C. A fürdő szabad felületén sikló cseppek lassulása. J. Fluid Mech. 803, 313–331 (2016).

Piroird, K., Clanet, C. és Quéré, D. a leidenfrost cseppek mágneses ellenőrzése. Phys. Jel. E 85, 056311 (2012).

Pandey, A., Nawijn, C. L. & Snoeijer, J. H. Hydrogel menisci: forma, kölcsönhatás és instabilitás. EPL 122, 36006 (2018).

Landau, L. D. és Lifshitz, E. M. Elméleti fizika tanfolyam, Mechanika 1. kötet. (Pergamon Press, Oxford, 1960).

Bertrand, J. Théorème relatif auouou d’un point attiré vers un center fixe. Comptes Rendus Acad. Sci. 77, 849–853 (2018).

Chin, S. A. Bertrand tételének valóban elemi bizonyítéka. Am. J. Phys. 83., 320–323 (2015).

Demirci, U. & Montesano, G. Sejteket kapszulázó cseppek üvegesítése. Labor. Forgács 7, 1428–1433 (2007).

Dou, R., Saunders, R., Mohamet, L., Ward, C. & Derby, B. A sejtek nagy áteresztőképességű krioprezerválása a részcseppek gyors fagyasztásával tintasugaras nyomtatással-krioprinteléssel. Labor. Forgács 15, 3503–3513 (2015).

Rall, W. F. & Fahy, G. M. egér embriók jégmentes krioprezerválása -196 ° C-on üvegesítéssel. Természet 313, 573–575 (1985).

Köszönetnyilvánítás

A szerzők köszönetet mondanak Rémi Proville-nek a cseppkövető algoritmusban nyújtott segítségért és Detlef Lohse-nak az értékes beszélgetésért.

Szerzői információk

Hovatartozások

A folyadékcsoport és a Max Plank Center Twente fizikája. Mesa + Intézet és Természettudományi és Technológiai Kar, J. M. Burgers Center for Fluid Dynamics és Max Plank Center Twente for Complex Fluid Dynamics, University of Twente, P.O. Box 217, 7500 AE, Enschede, Hollandia

Anaïs Gauthier, Devaraj van der Meer, Jacco H. Snoeijer és Guillaume Lajoinie

A PubMed Google Scholar alkalmazásban is kereshet erre a szerzőre

Hozzájárulások

A.G., D.v.d.M., J.H.S. és G.L. tervezték a kutatást, A.G. és G.L. végezték a kísérleteket, A.G., D.v.d.M., J.H.S. és G.L. elemezték és felépítették a modellt, A.G., D.v.d.M., J.H.S. és G.L.

Levelező szerzők

Etikai nyilatkozatok

Versenyző érdekek

A szerzők kijelentik, hogy nincsenek versengő érdekeik.

További információ

Peer review információk: A Nature Communications köszönetet mond az anonim bírálóknak a munka szakértői értékeléséhez való hozzájárulásukért.

A kiadó megjegyzése: A Springer Nature semleges marad a közzétett térképeken és az intézményi kapcsolatokban szereplő joghatósági igények tekintetében.