Értékelje a megtanult jellemzők pontosságát a vizsgálati adatokon - MATLAB

Értékelje a megtanult jellemzők pontosságát a tesztadatokon

Szintaxis

tévedés = veszteség (mdl, X, Y)
tévedés = veszteség (mdl, X, Y, név, érték)

Leírás

err = veszteség (mdl, X, Y) az átlagos négyzetbeli hibát adja vissza az err pontosságának mértékeként, az mdl modell esetében a prediktor értékeket X-ben és a válaszértékeket Y-ban .

err = veszteség (mdl, X, Y, név, érték) a pontosság mértékét adja vissza, err, a Név, érték pár argumentum által megadott kiegészítő opcióval.

Beviteli érvek

mdl - Szomszédsági komponens elemzési modell a regresszióhoz
FeatureSelectionNCARegression objektum

Szomszédsági elemzési modell a regresszióhoz, FeatureSelectionNCARegression objektumként megadva.

X - Prediktor változó értékek
n-by-p mátrix

Prediktor változó értékek, n-by-p mátrixként megadva, ahol n a megfigyelések száma és p a prediktor változók száma.

Adattípusok: egyetlen | kettős

Y - Válaszértékek
n hosszúságú numerikus valós vektor

Válaszértékek, amelyek n hosszúságú numerikus valós vektorként vannak megadva, ahol n a megfigyelések száma.

Adattípusok: egyetlen | kettős

Név-érték pár érvek

Adjon meg opcionálisan vesszővel elválasztott Név, Érték argumentumokat. A név az argumentum neve, az Érték pedig a megfelelő érték. A névnek idézőjelek között kell szerepelnie. Több név- és értékpár argumentumot megadhat bármilyen sorrendben: Név1, Érték1. Név, ÉrtékN .

'LossFunction' - Loss funkció típusa
'mse' (alapértelmezett) | 'őrült'

Veszteségfüggvény típusa, vesszővel elválasztott párként megadva, amely a „Loss Function” és az alábbiak egyikét tartalmazza.

Loss Function TypeDescription

„mse”	Átlagos négyzethiba
'őrült'	Átlagos abszolút eltérés

Példa: 'LossFunction', 'mse'

Kimeneti érvek

err - Kisebb-jobb pontosságmérő a megtanult tulajdonságok súlyához
skaláris érték

Kisebb, annál jobb pontossági mérték a megtanult jellemző súlyokhoz, skaláris értékként adva meg. A pontosság mértékét a LossFunction név-érték pár argumentummal adhatja meg.

Példák

Állítsa be az NCA modellt a regresszióhoz veszteség és előrejelzés segítségével

Töltse be a minta adatait.

Töltse le a ház adatait [1] az UCI Machine Learning Repository-ból [2]. Az adatkészlet 506 megfigyeléssel rendelkezik. Az első 13 oszlop tartalmazza a prediktor értékeket, az utolsó pedig a válaszértékeket. A cél a Boston külvárosában a tulajdonosok által használt lakások mediánértékének megjóslása 13 előrejelző függvényében.

Töltse be az adatokat, és határozza meg a válaszvektort és a prediktor mátrixot.

Ossza fel az adatokat oktatási és tesztkészletekre, a 4. prediktort használva a rétegzett particionálás csoportosító változójaként. Ez biztosítja, hogy minden partíció hasonló mennyiségű megfigyelést tartalmazzon az egyes csoportoktól.

A cvpartition véletlenszerűen 56 megfigyelést rendel hozzá egy tesztkészlethez, a többi adatot pedig egy edzéskészlethez.

Végezze el a funkciók kiválasztását az alapértelmezett beállítások használatával

Végezze el a jellemzők kiválasztását az NCA modell segítségével a regresszióhoz. Szabványosítsa a prediktor értékeket.

Ábrázolja a jellemző súlyokat.

A lényegtelen tulajdonságok súlya várhatóan megközelíti a nullát. Az fsrnca két jellemzőt irrelevánsként azonosít.

Számítsa ki a regressziós veszteséget.

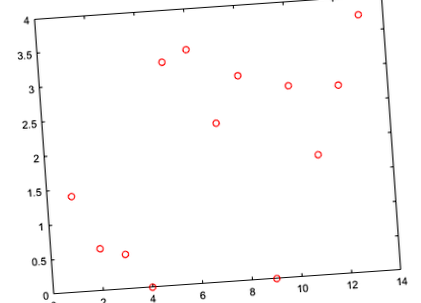
Számítsa ki a tesztkészlet előre jelzett válaszértékeit, és ábrázolja azokat a tényleges válasz függvényében.

A tökéletes illeszkedés a tényleges értékekkel szemben 45 fokos egyeneset alkot. Ebben a diagramban az előre jelzett és a tényleges válaszértékek szétszóródnak ezen a vonalon. A λ (szabályozási paraméter) értékének hangolása általában segít a teljesítmény javításában.

Tízszeres keresztellenőrzéssel hangolja be a szabályozási paramétert

A λ hangolása azt a λ érték megtalálását jelenti, amely a minimális regressziós veszteséget eredményezi. Íme a λ hangolásának lépései tízszeres keresztellenőrzéssel:

1. Először ossza fel az adatokat 10-szeresére. Minden hajtásnál a cvpartition az adatok 1/10-ét hozzárendeli edzéskészletként, és az adatok 9/10-ét tesztkészletként.

Rendelje hozzá a keresés λ értékeit. Hozzon létre egy tömböt a veszteségértékek tárolásához.

2. Vonatozza a szomszédsági komponens elemzés (nca) modelljét minden λ értékre az egyes hajtásokban beállított edzéskészlet segítségével.

3. Illesszen be egy Gauss-folyamat-regressziós (gpr) modellt a kiválasztott funkciók felhasználásával. Ezután a gpr modell segítségével számítsa ki a hajtás megfelelő tesztkészletének regressziós veszteségét. Jegyezze fel a veszteség értékét.

4. Ismételje meg ezt az egyes λ értékeknél és minden hajtásnál.

Számítsa ki a redőkből származó átlagos veszteséget minden λ értékre. Ábrázolja az átlagos veszteséget a λ értékekkel szemben.

Keresse meg a minimális veszteségértéket előállító λ értéket.

Hajtsa végre a regresszió jellemzőválasztását a legjobb λ érték használatával. Szabványosítsa a prediktor értékeket.