Osztályozási veszteség a Gauss-rendszermag osztályozási modelljéhez - MATLAB veszteség
Osztályozási veszteség a Gauss-rendszermag osztályozási modelljéhez
Szintaxis
Leírás
L = veszteség (Mdl, X, Y) a bináris Gauss-mag kiosztási modell Mdl osztályozási veszteségét adja vissza az X előrejelző adatait és az Y megfelelő osztálycímkéit felhasználva. .
L = veszteség (Mdl, Tbl, ResponseVarName) az Mdl modell osztályozási veszteségét adja vissza a Tbl előrejelző adatait és a Tbl valós osztálycímkéit használva. .
L = veszteség (Mdl, Tbl, Y) az Mdl modell osztályozási veszteségét adja vissza, a Tbl táblázat prediktor adatait és Y .
L = veszteség (___, Név, Érték) olyan opciókat határoz meg, amelyek egy vagy több név-érték pár argumentumot használnak a korábbi szintaxisok bármelyik bemeneti argumentum kombinációján kívül. Megadhat például egy osztályozási veszteségfüggvényt és megfigyelési súlyokat. Ezután a veszteség a súlyozott besorolási veszteséget adja vissza a megadott veszteségfüggvény segítségével.
Példák
Becsülje meg a tesztkészlet szerinti osztályozási veszteséget
Töltse be az ionoszféra adatsort. Ennek az adatsornak 34 prediktora és 351 bináris válasza van a radar visszatérésére, rossz ('b') vagy jó ('g').
Ossza be az adatkészletet képzési és tesztkészletekbe. Adjon meg egy 15% -os tartási mintát a tesztkészlethez.
A bináris kernel osztályozási modell képzése a képzési készlet használatával.
Becsülje meg az edzéskészlet osztályozási hibáját és a tesztkészlet osztályozási hibáját.
Adja meg az egyéni osztályozási veszteséget
Töltse be az ionoszféra adatsort. Ennek az adatsornak 34 prediktora és 351 bináris válasza van a radar visszatérésére, rossz ('b') vagy jó ('g').
Ossza be az adatkészletet képzési és tesztkészletekbe. Adjon meg egy 15% -os tartási mintát a tesztkészlethez.
A bináris kernel osztályozási modell képzése a képzési készlet használatával.
Hozzon létre egy névtelen függvényt, amely méri a lineáris veszteséget,
L = ∑ j - w j y j f j ∑ j w j .
w j a j megfigyelés súlya, y j a j válasz (-1 a negatív osztályra és 1 egyébként), és f j a j megfigyelés nyers osztályozási pontszáma .
Az egyedi veszteségfüggvényeket meghatározott formában kell megírni. Az egyéni veszteségfüggvény megírásának szabályait lásd a 'LossFun' név-érték pár argumentumban.
Becsülje meg az edzéskészlet osztályozási veszteségét és a tesztkészlet osztályozási veszteségét a lineáris veszteségfüggvény segítségével.
Beviteli érvek
Mdl - bináris kernelminősítési modell
ClassificationKernel modell objektum
Bináris rendszermag osztályozási modell, ClassificationKernel modell objektumként megadva. A fitckernel használatával létrehozhat egy ClassificationKernel modellobjektumot .
X - Jósló adatok
n-pp numerikus mátrix
Prediktor adatok, n-pp numerikus mátrixként megadva, ahol n a megfigyelések száma és p az Mdl képzésére használt prediktorok száma .
Y hosszának és az X-ben megfigyelt megfigyelések számának meg kell egyeznie.
Adattípusok: egyetlen | kettős
Y - Osztálycímkék
kategorikus tömb | karaktertömb | string tömb | logikai vektor | numerikus vektor | karaktervektorok sejttömbje
Osztálycímkék, kategorikus, karakter vagy karakterlánc tömbként, logikai vagy numerikus vektorként vagy karaktervektor cellatömbként megadva.
Az Y adattípusának meg kell egyeznie az Mdl.ClassNames adattípusával. (A szoftver a karakterlánc-tömböket karaktervektorok cellatömbjeként kezeli.)
Az Y különálló osztályainak az Mdl.ClassNames részhalmazának kell lenniük .
Ha Y karaktertömb, akkor minden elemnek meg kell felelnie a tömb egy sorának.
Az Y hosszának meg kell egyeznie az X-ben vagy a Tbl-ben észlelt megfigyelések számával .
Adattípusok: kategorikus | char | húr | logikus | egyetlen | kettős | sejt
Tbl - Mintaadatok
asztal
A modell kiképzéséhez használt mintadatok, táblázatként megadva. A Tbl minden sora egy megfigyelésnek felel meg, és minden oszlop egy prediktor változónak felel meg. Opcionálisan a Tbl tartalmazhat további oszlopokat a válaszváltozóhoz és a megfigyelési súlyokhoz. A Tbl-nek tartalmaznia kell az Mdl képzéséhez használt összes prediktort. A többoszlopos változók és a karaktervektorok sejttömbjeitől eltérő sejttömbök nem megengedettek.
Ha a Tbl tartalmazza az Mdl képzéséhez használt válaszváltozót, akkor nem kell megadnia a ResponseVarName vagy Y .
Ha az Mdl-t egy táblázatban található mintaadatok felhasználásával edzi, akkor a veszteségre vonatkozó bemeneti adatoknak is táblázatban kell lenniük.
ResponseVarName - Válaszváltozó neve
változó neve a Tbl-ben
Válaszváltozó neve, a Tbl változó neveként megadva. Ha a Tbl tartalmazza az Mdl képzéséhez használt válaszváltozót, akkor nem kell megadnia a ResponseVarName nevet .
Ha megadja a ResponseVarName nevet, akkor karaktervektorként vagy karakterlánc skalárként kell megadnia. Például, ha a válaszváltozó Tbl.Y néven van tárolva, akkor adja meg a ResponseVarName nevet „Y” -ként. Egyébként a szoftver a Tbl összes oszlopát, beleértve a Tbl.Y-t is, prediktorként kezeli.
A válaszváltozónak kategorikusnak, karakter- vagy karakterlánc-tömbnek, logikai vagy numerikus vektornak vagy karaktervektor-cellatömbnek kell lennie. Ha a válaszváltozó karaktertömb, akkor minden elemnek meg kell felelnie a tömb egy sorának.
Adattípusok: char | húr
Név-érték pár érvek
Adjon meg opcionálisan vesszővel elválasztott Név, Érték argumentumokat. A név az argumentum neve, az Érték pedig a megfelelő érték. A névnek idézőjelek között kell szerepelnie. Több név- és értékpár argumentumot megadhat bármilyen sorrendben: Név1, Érték1. Név, ÉrtékN .
Példa: L = veszteség (Mdl, X, Y, „LossFun”, „másodfokú”, „Súlyok”, súlyok) a súlyozott osztályozási veszteséget adja vissza a másodfokú veszteségfüggvény segítségével.
'LossFun' - Veszteség funkció
'classsiferror' (alapértelmezett) | „binodeviance” | „exponenciális” | „zsanér” | "logit" | „mincost” | „másodfokú” | funkció fogantyú
Veszteségfüggvény, vesszővel elválasztott párként megadva, amely a „LossFun” és a beépített veszteségfüggvény nevéből vagy függvényfogantyúból áll.
Ez a táblázat az elérhető veszteségfüggvényeket sorolja fel. Adjon meg egyet a megfelelő értékkel.
| „binodeviance” | Binomiális eltérés |
| 'classsiferror' | Osztályozási hiba |
| „exponenciális” | Exponenciális |
| 'zsanér' | Zsanér |
| „logit” | Logisztikai |
| „mincost” | Minimális várható téves osztályozási költség (a hátsó valószínűségű osztályozási pontszámoknál) |
| 'négyzetes' | Négyzetes |
A „mincost” alkalmas az utólagos valószínűségű osztályozási pontszámokra. A rendszermag-osztályozási modelleknél a logisztikus regressziós tanulók alapértelmezés szerint osztályozási pontszámként adják vissza a hátsó valószínűségeket, az SVM-tanulók azonban nem (lásd előrejelzés).
Adja meg saját függvényét a függvény fogantyújának jelölésével.
Legyen n az X-ben megfigyelések száma, K pedig a különálló osztályok száma (numel (Mdl.ClassNames), ahol az Mdl a bemeneti modell). A funkciójának a következő aláírással kell rendelkeznie:
A kimeneti argumentum veszteségértéke skalár.
Kiválasztja a függvény nevét (lossfun).
C egy n -by-K logikai mátrix, sorokkal jelezve azt az osztályt, amelyhez a megfelelő megfigyelés tartozik. Az oszlopok sorrendje megfelel az Mdl.ClassNames osztályrendi sorrendnek .
Szerkessze C-t a C (p, q) = 1 beállításával, ha a p megfigyelés a q osztályba tartozik, minden sorhoz. Állítsa a p sor összes többi elemét 0-ra .
S az osztályozási pontszámok n-by-K numerikus mátrixa. Az oszlopok sorrendje megfelel az Mdl.ClassNames osztályrendi sorrendnek. S az osztályozási pontszámok mátrixa, hasonlóan a jóslás kimenetéhez .
W a megfigyelési súlyok n-by-1 numerikus vektora. Ha elhalad W-n, a szoftver normalizálja a súlyokat, hogy összeadódjanak 1-re .
A költség a téves osztályozási költségek K-by-K numerikus mátrixa. Például a Költség = egyek (K) - szem (K) értéke 0 a helyes osztályozáshoz, 1 pedig a téves osztályozáshoz.
Példa: 'LossFun', @ lossfun
Adattípusok: char | húr | function_handle
„Súlyok” - Megfigyelési súlyok
egyesek (méret (X, 1), 1) (alapértelmezett) | numerikus vektor | változó neve a Tbl-ben
Megfigyelési súlyok, vesszővel elválasztott párként megadva, amely „Súlyok” -ból és egy numerikus vektorból vagy egy változó nevéből áll a Tbl-ben .
Ha a Súlyok numerikus vektor, akkor a Súlyok méretének meg kell egyeznie az X vagy Tbl sorok számával .
Ha a Súly a változó neve a Tbl-ben, meg kell adnia a súlyokat karaktervektorként vagy karakterlánc skalárként. Például, ha a súlyokat Tbl.W néven tároljuk, akkor a Súlyokat adja meg „W” néven. Egyébként a szoftver a Tbl összes oszlopát, beleértve a Tbl.W-t is, prediktorként kezeli.
Ha súlyokat ad meg, akkor a veszteség kiszámítja a súlyozott osztályozási veszteséget és normalizálja a súlyokat, hogy összeadódjanak az adott osztály korábbi valószínűségének értékével.
Adattípusok: kettős | egyetlen | char | húr
Kimeneti érvek
L - Osztályozási veszteség
numerikus skalár
Osztályozási veszteség, numerikus skalárként visszaadva. Az L értelmezése a súlyoktól és a LossFun függvénye .
További információ
Osztályozási veszteség
Az osztályozási veszteségfüggvények az osztályozási modellek prediktív pontatlanságát mérik. Ha összehasonlítja az azonos típusú veszteségeket sok modell között, az alacsonyabb veszteség jobb prediktív modellt jelez.
Tegyük fel a következőket:
L az osztályozási veszteség súlyozott átlaga.
n a minta mérete.
yj a megfigyelt osztálycímke. A szoftver –1 vagy 1-ként kódolja, jelezve a negatív vagy a pozitív osztályt.
f (Xj) az X előrejelző adat transzformált j megfigyelésének (sorának) nyers osztályozási pontszáma a jellemzők bővítésével.
mj = yj f (Xj) a j megfigyelés osztályozása az yj-nek megfelelő osztályba. Az mj pozitív értékei a helyes osztályozást jelzik, és nem járulnak hozzá sokat az átlagos veszteséghez. Az mj negatív értékei helytelen osztályozást jeleznek, és hozzájárulnak az átlagos veszteséghez.
A j megfigyelés súlya wj. A szoftver normalizálja a megfigyelési súlyokat úgy, hogy azok összeadódjanak a megfelelő korábbi osztály valószínűséggel. A szoftver az előzetes valószínűségeket is normalizálja, így azok összege 1. Ezért,
Ez a táblázat ismerteti azokat a támogatott veszteségfüggvényeket, amelyeket a „LossFun” név-érték pár argumentummal határozhat meg.
L = ∑ j = 1 n w j I < y ^ j ≠ y j >.
Az osztályozási hiba a rosszul osztályozott megfigyelések súlyozott hányada, ahol y ^ j a maximális hátsó valószínűségű osztálynak megfelelő osztálycímke. én< x> az indikátor funkció.
A szoftver ezzel az eljárással kiszámítja a súlyozott minimális költségeket a j = 1. n megfigyelésekhez.
Becsülje meg a j megfigyelés várható osztályozási költségeinek 1-by-K vektorát:
γ j = f (X j) ′ C .
f (Xj) az osztály hátsó valószínűségeinek oszlopvektora. C az a költségmátrix, amelyet az input modell a Cost tulajdonságban tárol.
J megfigyelés esetén jósolja meg a minimális várható osztályozási költségnek megfelelő osztálycímkét:
y ^ j = min j = 1,., K (γ j) .
A C segítségével azonosítsa az előrejelzéshez kapcsolódó költségeket (cj).
A súlyozott, átlagos, minimális költségveszteség
L = ∑ j = 1 n w j c j .
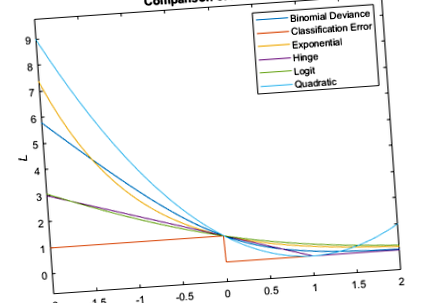
Ez az ábra összehasonlítja a veszteségfüggvényeket (a minimális költség kivételével) egy m feletti megfigyelésnél. Néhány funkció normalizálva van [0,1].
Kiterjesztett képességek
Magas tömbök
Számoljon tömbökkel, amelyeknek több sora van, mint amennyit a memóriában elférnek.
Használati megjegyzések és korlátozások:
veszteség nem támogatja a magas asztal adatait.
További információ: Tall Arrays.
Lásd még
Nyissa meg a Példa lehetőséget
Ennek a példának a módosított verziója létezik a rendszerén. Meg akarja nyitni ezt a verziót?
- Osztályozási veszteség lineáris osztályozási modellekhez - MATLAB
- Az elhízás osztályozása személyre szabott étrendi fogyáskezelés alapján
- GitHub - optomcWeight-loss-MC MCML-alapú MATLAB hordozott súlycsökkentő MC-modell az érvényesítéshez
- Definiálja az egyedi súlyozott osztályozási réteget - MATLAB; Simulink
- Definiálja az egyéni edzésköröket, a veszteségfüggvényeket és a hálózatokat - MATLAB; Simulink