Osztályozási veszteség lineáris osztályozási modellekhez

Szintaxis

Leírás

L = veszteség (Mdl, X, Y) az bináris, lineáris osztályozási modell Mdl osztályozási veszteségeit adja eredményül, X előrejelző és Y megfelelő osztálycímkék felhasználásával. L az osztályozási hibaarányokat tartalmazza az egyes szabályozási erősségekhez Mdl-ben .

L = veszteség (Mdl, Tbl, ResponseVarName) a Tbl előrejelző adatok és a Tbl valós osztálycímkék osztályozási veszteségeit adja eredményül. .

L = veszteség (Mdl, Tbl, Y) a Tbl táblázatban szereplő prediktor adatok osztályozási veszteségeit és Y .

L = veszteség (___, Név, Érték) olyan opciókat határoz meg, amelyek egy vagy több név-érték pár argumentumot használnak a korábbi szintaxisok bármelyik bemeneti argumentum kombinációján kívül. Megadhatja például, hogy az előrejelző adatok oszlopai megfelelnek-e a megfigyeléseknek, vagy megadhatja az osztályozási veszteség függvényét.

Beviteli érvek

Mdl - bináris, lineáris osztályozási modell
Lineáris modell objektum

Bináris, lineáris osztályozási modell, ClassificationLinear modell objektumként megadva. A fitclinear használatával létrehozhat egy ClassificationLinear modellobjektumot .

X - Jósló adatok
teljes mátrix | ritka mátrix

Prediktor adatok, n-by p teljes vagy ritka mátrixként megadva. Ez az X orientáció azt jelzi, hogy a sorok megfelelnek az egyes megfigyeléseknek, az oszlopok pedig az egyes prediktor változóknak.

jegyzet

Y hosszának és az X-ben megfigyelt megfigyelések számának meg kell egyeznie.

Adattípusok: egyetlen | kettős

Y - Osztálycímkék
kategorikus tömb | karaktertömb | string tömb | logikai vektor | numerikus vektor | karaktervektorok sejttömbje

Osztálycímkék, kategorikus, karakter vagy karakterlánc tömbként, logikai vagy numerikus vektorként vagy karaktervektor cellatömbként megadva.

Az Y adattípusának meg kell egyeznie az Mdl.ClassNames adattípusával. (A szoftver a karakterlánc-tömböket karaktervektorok cellatömbjeként kezeli.)

Az Y különálló osztályainak az Mdl.ClassNames részhalmazának kell lenniük .

Ha Y karaktertömb, akkor minden elemnek meg kell felelnie a tömb egy sorának.

Az Y hosszának meg kell egyeznie az X-ben vagy a Tbl-ben észlelt megfigyelések számával .

Tbl - Mintaadatok
asztal

A modell kiképzéséhez használt mintadatok, táblázatként megadva. A Tbl minden sora egy megfigyelésnek felel meg, és minden oszlop egy prediktor változónak felel meg. Opcionálisan a Tbl tartalmazhat további oszlopokat a válaszváltozóhoz és a megfigyelési súlyokhoz. A Tbl-nek tartalmaznia kell az Mdl képzéséhez használt összes prediktort. A többoszlopos változók és a karaktervektorok sejttömbjeitől eltérő sejttömbök nem megengedettek.

Ha a Tbl tartalmazza az Mdl képzéséhez használt válaszváltozót, akkor nem kell megadnia a ResponseVarName vagy Y .

Ha az Mdl-t egy táblázatban található mintaadatok felhasználásával edzi, akkor a veszteségre vonatkozó bemeneti adatoknak is táblázatban kell lenniük.

ResponseVarName - Válaszváltozó neve
változó neve a Tbl-ben

Válaszváltozó neve, a Tbl változó neveként megadva. Ha a Tbl tartalmazza az Mdl képzéséhez használt válaszváltozót, akkor nem kell megadnia a ResponseVarName nevet .

Ha megadja a ResponseVarName nevet, akkor karaktervektorként vagy karakterlánc skalárként kell megadnia. Például, ha a válaszváltozó Tbl.Y néven van tárolva, akkor adja meg a ResponseVarName nevet „Y” -ként. Egyébként a szoftver a Tbl összes oszlopát, beleértve a Tbl.Y-t is, prediktorként kezeli.

A válaszváltozónak kategorikusnak, karakter- vagy karakterlánc-tömbnek, logikai vagy numerikus vektornak vagy karaktervektor-cellatömbnek kell lennie. Ha a válaszváltozó karaktertömb, akkor minden elemnek meg kell felelnie a tömb egy sorának.

Adattípusok: char | húr

Név-érték pár érvek

Adjon meg opcionálisan vesszővel elválasztott Név, Érték argumentumokat. A név az argumentum neve, az Érték pedig a megfelelő érték. A névnek idézőjelek között kell szerepelnie. Több név- és értékpár argumentumot megadhat bármilyen sorrendben: Név1, Érték1. Név, ÉrtékN .

'LossFun' - Veszteség funkció
'classsiferror' (alapértelmezett) | „binodeviance” | „exponenciális” | „zsanér” | "logit" | „mincost” | „másodfokú” | funkció fogantyú

Veszteségfüggvény, vesszővel elválasztott párként megadva, amely „LossFun” -ból és egy beépített veszteségfüggvény-névből vagy függvényfogantyúból áll.

Az alábbi táblázat az elérhető veszteségfüggvényeket sorolja fel. Adjon meg egyet a megfelelő karakter vektorral vagy karakterlánc skalárral.

ValueDescription

„binodeviance”	Binomiális eltérés
'classsiferror'	Osztályozási hiba
„exponenciális”	Exponenciális
'zsanér'	Zsanér
„logit”	Logisztikai
„mincost”	Minimális várható téves osztályozási költség (a hátsó valószínűségű osztályozási pontszámoknál)
'négyzetes'	Négyzetes

A „mincost” alkalmas az utólagos valószínűségű osztályozási pontszámokra. Lineáris osztályozási modellek esetén a logisztikus regressziós tanulók alapértelmezés szerint osztályozási pontszámként adják vissza a hátsó valószínűségeket, az SVM-tanulók azonban nem (lásd előrejelzés).

Adja meg saját függvényét a függvény fogantyújának jelölésével.

Legyen n az X-ben megfigyelések száma, K pedig a különálló osztályok száma (numel (Mdl.ClassNames), ahol az Mdl a bemeneti modell). A funkciójának a következő aláírással kell rendelkeznie:

A kimeneti argumentum veszteségértéke skalár.

Kiválasztja a függvény nevét (lossfun).

C egy n -by-K logikai mátrix, sorokkal jelezve azt az osztályt, amelyhez a megfelelő megfigyelés tartozik. Az oszlopok sorrendje megfelel az Mdl.ClassNames osztályrendi sorrendnek .

Szerkessze C-t a C (p, q) = 1 beállításával, ha a p megfigyelés a q osztályba tartozik, minden sorhoz. Állítsa a p sor összes többi elemét 0-ra .

S az osztályozási pontszámok n-by-K numerikus mátrixa. Az oszlopok sorrendje megfelel az Mdl.ClassNames osztályrendi sorrendnek. S az osztályozási pontszámok mátrixa, hasonlóan a jóslás kimenetéhez .

W a megfigyelési súlyok n-by-1 numerikus vektora. Ha elhalad W-n, a szoftver normalizálja a súlyokat, hogy összeadódjanak 1-re .

A költség a téves osztályozási költségek K-by-K numerikus mátrixa. Például a Költség = egyek (K) - szem (K) értéke 0 a helyes osztályozáshoz, 1 pedig a téves osztályozáshoz.

Példa: 'LossFun', @ lossfun

Adattípusok: char | húr | function_handle

'ObservationsIn' - A prediktor adatmegfigyelési dimenziója
"sorok" (alapértelmezett) | 'oszlopok'

Prediktor adatmegfigyelési dimenzió, vesszővel elválasztott párként megadva, amely „ObservationsIn” és „oszlopok” vagy „sorok ”ból áll .

jegyzet

Ha a prediktor mátrixot úgy orientálja, hogy a megfigyelések megfeleljenek az oszlopoknak, és megadja az „ObservationsIn”, „oszlopok” elemeket, akkor jelentősen csökkenhet az optimalizálás végrehajtási ideje. Nem lehet megadni a „ObservationsIn”, „oszlopok” előrejelző adatokat egy táblázatban.

„Súlyok” - Megfigyelési súlyok
egyesek (méret (X, 1), 1) (alapértelmezett) | numerikus vektor | változó neve a Tbl-ben

Megfigyelési súlyok, vesszővel elválasztott párként megadva, amely „Súlyok” -ból és egy numerikus vektorból vagy egy változó nevéből áll a Tbl-ben .

Ha megadja a Súlyokat numerikus vektorként, akkor a Súlyok méretének meg kell egyeznie az X vagy Tbl megfigyelések számával .

Ha a súlyokat a változó neveként adja meg a Tbl-ben, akkor a névnek karaktervektornak vagy karakterlánc-skalárnak kell lennie. Például, ha a súlyokat Tbl.W néven tároljuk, akkor a Súlyokat adja meg „W” néven. Egyébként a szoftver a Tbl összes oszlopát, beleértve a Tbl.W-t is, prediktorként kezeli.

Ha súlyokat ad meg, akkor minden szabályozási erősséghez a veszteség kiszámítja a súlyozott osztályozási veszteséget és normalizálja a súlyokat, hogy összeadódjanak az adott osztály előzetes valószínűségének értékével.

Adattípusok: kettős | egyetlen

Kimeneti érvek

L - Osztályozási veszteségek
numerikus skalár | numerikus sor vektor

Osztályozási veszteségek, számszerű skalár vagy sorvektorként visszaadva. Az L értelmezése a súlyoktól és a LossFun függvénye .

L azonos méretű, mint az Mdl.Lambda. L (j) az Mdl szabályozási szilárdság felhasználásával kiképzett lineáris osztályozási modell osztályozási vesztesége. Lambda (j) .

Példák

Becsülje meg a teszt-minta osztályozási veszteséget

Töltse be az NLP adatsort.

X az előrejelző adatok gyér mátrixa, Y pedig az osztálycímkék kategorikus vektora. Az adatokban több mint két osztály található.

A modelleknek azonosítaniuk kell, hogy a weboldalon szereplő szavak száma a Statistics and Machine Learning Toolbox ™ dokumentációból származik-e. Tehát azonosítsa azokat a címkéket, amelyek megfelelnek a Statistics és Machine Learning Toolbox ™ dokumentációs weboldalainak.

Készítsen bináris, lineáris osztályozási modellt, amely azonosíthatja, hogy a szó számít-e egy dokumentációs weboldalon, a Statistics and Machine Learning Toolbox ™ dokumentációból. Adja meg, hogy a megfigyelések 30% -át kitartsa. Optimalizálja a célfüggvényt a SpaRSA segítségével.

A CVMdl egy ClassificationPartitionedLinear modell. Ez tartalmazza a Tréning tulajdonságot, amely egy egy az egyben cellatömb, amely egy ClassificationLinear modellt tartalmaz, amelyet a szoftver képzett az oktatási készlet segítségével.

Vegye ki az edzés és a teszt adatait a partíció meghatározásából.

Becsülje meg az edzés- és tesztminta osztályozási hibát.

Mivel a CMdl-ben egy szabályozási erősség van, a ceTrain és a ceTest numerikus skalárok.

Adja meg az egyéni osztályozási veszteséget

Töltse be az NLP adatsort. Feldolgozza az adatokat az Estimate Test-Sample Classification Loss szerint, és helyezze át a prediktor adatait.

Képezzen bináris, lineáris osztályozási modellt. Adja meg, hogy a megfigyelések 30% -át kitartsa. Optimalizálja a célfüggvényt a SpaRSA segítségével. Adja meg, hogy a prediktor megfigyelések megfelelnek-e az oszlopoknak.

Vegye ki az edzés és a teszt adatait a partíció meghatározásából.

Hozzon létre egy névtelen függvényt, amely méri a lineáris veszteséget,

L = ∑ j - w j y j f j ∑ j w j .

w j a j megfigyelés súlya, y j a j válasz (-1 a negatív osztályra és 1 egyébként), és f j a j megfigyelés nyers osztályozási pontszáma. Az egyedi veszteségfüggvényeket meghatározott formában kell megírni. Az egyéni veszteségfüggvény megírásának szabályait lásd a LossFun név-érték pár argumentumban.

Becsülje meg az edzés- és tesztminta osztályozási veszteségét a lineáris veszteségfüggvény segítségével.

Találja meg a jó lasszó büntetést az osztályozási veszteség felhasználásával

A logisztikai regressziós tanulót használó lineáris osztályozási modell jó lasszóbüntetés-erősségének meghatározásához hasonlítsa össze a tesztminta besorolási hibaarányait.

Töltse be az NLP adatsort. Az adatok előkészítése az Egyéni osztályozási veszteség megadása részben leírtak szerint.

Készítsen 11 logaritmikusan elosztott szabályozási erősség halmazát 1 0 - 6 és 1 0 - 0 között. 5. .

Vonatozzon bináris, lineáris osztályozási modelleket, amelyek az egyes szabályozási erősségeket használják. Optimalizálja a célfüggvényt a SpaRSA segítségével. Engedje le a célfüggvény gradiensének tűrését 1e-8-ra .

Bontsa ki a képzett lineáris osztályozási modellt.

Az Mdl egy ClassificationLinear modell objektum. Mivel a Lambda a szabályozási erősségek szekvenciája, az Mdl-re 11 modellként gondolhatunk, egy-egy a Lambda minden egyes szabályozási erősségére .

Becsülje meg a tesztminta osztályozási hibáját.

Mivel 11 szabályozási erősség létezik, a ce egy 11-szeres vektor a besorolási hibaarányokról.

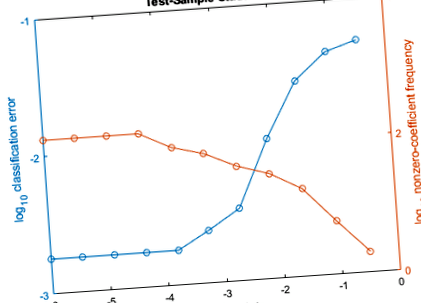
A Lambda magasabb értékei előrejelző változó ritkaságot eredményeznek, ami jó osztályozási osztály. Minden egyes szabályozási erősséghez képezzen egy lineáris osztályozási modellt a teljes adatkészlet és ugyanazok a lehetőségek felhasználásával, mint a modellek keresztvalidálásakor. Határozza meg a nem nulla együtthatók számát modellenként.

Ugyanazon az ábrán ábrázolja a tesztminta hibarátáit és a nem nulla együtthatók gyakoriságát minden egyes szabályozási erősséghez. Ábrázolja az összes változót a naplóskálán.

Válassza ki a szabályozás erősségének indexét, amely kiegyensúlyozza a prediktor változó ritkulását és az alacsony besorolási hibát. Ebben az esetben 1 0 - 4 és 1 0 - 1 közötti értéknek elegendőnek kell lennie.

Válassza ki a modellt az Mdl-ből a kiválasztott szabályosítási erővel.

Az MdlFinal egy ClassificationLinear modell, amely egy szabályosítási erőt tartalmaz. Az új megfigyelések címkéinek becsléséhez adja át az MdlFinal-t és az új adatokat az előrejelzéshez .

További információ

Osztályozási veszteség

Az osztályozási veszteségfüggvények az osztályozási modellek prediktív pontatlanságát mérik. Ha összehasonlítja az azonos típusú veszteségeket sok modell között, az alacsonyabb veszteség jobb prediktív modellt jelez.

Vegye figyelembe a következő forgatókönyvet.

L az osztályozási veszteség súlyozott átlaga.

n a minta mérete.

Bináris osztályozáshoz:

yj a megfigyelt osztálycímke. A szoftver –1 vagy 1-ként kódolja, jelezve a negatív vagy a pozitív osztályt.

f (Xj) az X előrejelző adatok j megfigyelésének (sor) nyers osztályozási pontszáma.

mj = yj f (Xj) a j megfigyelés osztályozása az yj-nek megfelelő osztályba. Az mj pozitív értékei a helyes osztályozást jelzik, és nem járulnak hozzá sokat az átlagos veszteséghez. Az mj negatív értékei helytelen osztályozást jeleznek, és jelentősen hozzájárulnak az átlagos veszteséghez.

A többosztályos osztályozást támogató algoritmusok (azaz K ≥ 3) esetén:

yj * a K - 1 nullák vektora, ahol 1 az igaz, megfigyelt yj osztálynak megfelelő helyzetben van. Például, ha a második megfigyelés valódi osztálya a harmadik osztály és K = 4, akkor y2 * = [0 0 1 0] ′. Az osztályok sorrendje megfelel a bemeneti modell ClassNames tulajdonságának sorrendjének.

f (Xj) az X előrejelző adatok j megfigyeléséhez tartozó osztályozási pontszámok K hosszúságú vektora. A pontszámok sorrendje megfelel az osztályok sorrendjének a bemeneti modell ClassNames tulajdonságában.

mj = yj * ′ f (Xj). Ezért mj az a skaláris osztályozási pontszám, amelyet a modell megjósol az igaz, megfigyelt osztályra.

A j megfigyelés súlya wj. A szoftver normalizálja a megfigyelési súlyokat úgy, hogy azok összeadódjanak a megfelelő korábbi osztály valószínűséggel. A szoftver normalizálja az előzetes valószínűségeket is, így ezek összege 1-re nő. Ezért,

Ennek a forgatókönyvnek az ismeretében az alábbi táblázat leírja azokat a támogatott veszteségfüggvényeket, amelyeket a 'LossFun' név-érték pár argumentummal határozhat meg.

L = ∑ j = 1 n w j I < y ^ j ≠ y j >.

Az osztályozási hiba a rosszul osztályozott megfigyelések súlyozott hányada, ahol y ^ j a maximális hátsó valószínűségű osztálynak megfelelő osztálycímke. én< x> az indikátor funkció.

A szoftver ezzel az eljárással kiszámítja a súlyozott minimális költségeket a j = 1. n megfigyelésekhez.

Becsülje meg a j megfigyelés várható osztályozási költségeinek 1-by-K vektorát:

γ j = f (X j) ′ C .

f (Xj) az osztály hátsó valószínűségének oszlopvektora a bináris és a többosztályos osztályozáshoz. C az a költségmátrix, amelyet az input modell a Cost tulajdonságban tárolt.

J megfigyelés esetén jósolja meg a minimális várható osztályozási költségnek megfelelő osztálycímkét:

y ^ j = min j = 1,., K (γ j) .

A C segítségével azonosítsa az előrejelzéshez kapcsolódó költségeket (cj).

A súlyozott, átlagos, minimális költségveszteség

L = ∑ j = 1 n w j c j .

Ez az ábra összehasonlítja a veszteségfüggvényeket (kivéve a „mincost”) egy m feletti megfigyelésnél. Néhány funkció normalizálva van [0,1].

Algoritmusok

Alapértelmezés szerint a megfigyelési súlyok korábbi osztály valószínűségek. Ha a súlyokat a Súlyok segítségével adja meg, akkor a szoftver normalizálja azokat, hogy összeadódjanak az adott osztályok korábbi valószínűségeivel. A szoftver a renormalizált súlyokat használja a súlyozott besorolási veszteség becsléséhez.

Osztályozási veszteség lineáris osztályozási modellekhez - MATLAB