Értékelje a megtanult jellemzők pontosságát a vizsgálati adatokon - MATLAB

Értékelje a megtanult jellemzők pontosságát a tesztadatokon

Szintaxis

tévedés = veszteség (mdl, X, Y)
tévedés = veszteség (mdl, X, Y, név, érték)

Leírás

err = veszteség (mdl, X, Y) kiszámítja az mdl modell téves osztályozási hibáját az X előrejelzőinek és az Y osztály osztálycímkéinek .

err = veszteség (mdl, X, Y, név, érték) kiszámítja az osztályozási hibát egy vagy több név, érték pár argumentum által megadott további opciókkal.

Beviteli érvek

mdl - Szomszédsági komponens elemzési modell az osztályozáshoz
FeatureSelectionNCAClassification objektum

Az osztályozáshoz használt szomszédsági komponenselemzési modell FeatureSelectionNCAClassification objektumként került visszaadásra.

X - Prediktor változó értékek
n-by-p mátrix

Prediktor változó értékek, n-by-p mátrixként megadva, ahol n a megfigyelések száma és p a prediktor változók száma.

Adattípusok: egyetlen | kettős

Y - Osztálycímkék
kategorikus vektor | logikai vektor | numerikus vektor | string tömb | n hosszú karaktervektorok sejttömbje n soros karaktermátrix

Osztálycímkék, kategorikus vektorként, logikai vektorként, numerikus vektorként, karakterlánc tömbként, n hosszúságú karaktervektorok cellatömbjeként vagy n soros karaktermátrixként, ahol n a megfigyelések száma. Y elem i vagy i sora az X. i sorának megfelelő osztálycímke (i megfigyelés).

Név-érték pár érvek

Adjon meg opcionálisan vesszővel elválasztott Név, Érték argumentumokat. A név az argumentum neve, az Érték pedig a megfelelő érték. A névnek idézőjelek között kell szerepelnie. Több név- és értékpár argumentumot megadhat bármilyen sorrendben: Név1, Érték1. Név, ÉrtékN .

'LossFunction' - Loss funkció típusa
'classsiferror' (alapértelmezett) | 'négyzetes'

Veszteségfüggvény típusa, vesszővel elválasztott párként megadva, amely a „Loss Function” és az alábbiak egyikét tartalmazza.

'classsiferror' - téves besorolási hiba, a következőképpen definiálva:

1 n ∑ i = 1 n I (k i ≠ t i),

ahol k i a megjósolt osztály, és t i az i megfigyelés igazi osztálya. Az I (k i ≠ t i) annak a mutatója, amikor a k i nem azonos a t i-vel .

„másodfokú” - Másodfokú veszteségfüggvény, a következőként definiálva

1 n ∑ i = 1 n ∑ k = 1 c (p i k - I (i, k)) 2,

ahol c az osztályok száma, p i k annak a becslésnek a valószínűsége, hogy az i-es megfigyelés a k osztályba tartozik, és I (i, k) az a mutató, hogy az i-es megfigyelés a k osztályba tartozik.

Példa: 'LossFunction', 'másodfokú'

Kimeneti érvek

err - Kisebb-jobb pontosságmérő a megtanult tulajdonságok súlyához
skaláris érték

Kisebb, annál jobb pontossági mérték a megtanult jellemző súlyokhoz, skaláris értékként adva meg. A pontosság mértékét a LossFunction név-érték pár argumentummal adhatja meg.

Példák

Tune NCA osztályozási modell

Töltse be a minta adatait.

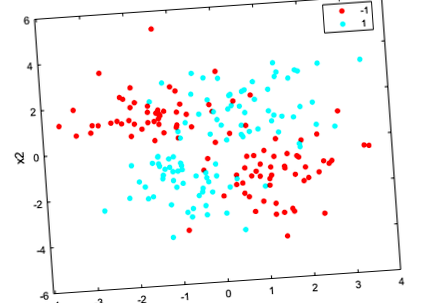
Hozzon létre egy szórási diagramot az adatok szerint osztályok szerint.

Adjon hozzá 100 irreleváns funkciót a következőhöz:. Először állítson elő adatokat egy Normal eloszlásból 0 átlaggal és 20 szórással.

Normalizálja az adatokat úgy, hogy az összes pont 0 és 1 között legyen.

Illesszen egy szomszédsági komponens-elemzési (NCA) modellt az adatokhoz az alapértelmezett Lambda (szabályozási paraméter,) értékkel. Használja az LBFGS megoldót, és jelenítse meg a konvergencia információkat.

Ábrázolja a jellemző súlyokat. A lényegtelen tulajdonságok súlyának nagyon közel kell lennie a nullához.

Jósolja meg az osztályokat az NCA modell segítségével, és számítsa ki a zavaros mátrixot.

A zavartsági mátrix azt mutatja, hogy a –1 osztályba tartozó adatok közül 40 előrejelzés szerint a –1 osztályba tartozik. Az előrejelzések szerint az –1 osztályba tartozó adatok 60-a az 1. osztályba tartozik. Hasonlóképpen, az 1. osztályba tartozó adatok közül 94 az 1. osztályba tartozik, közülük a 6. –1. A –1 osztály előrejelzési pontossága nem jó.

Minden súly nagyon közel áll a nullához, ami azt jelzi, hogy a modell edzésénél használt érték túl nagy. Amikor az összes jellemző súlya megközelíti a nullát. Ezért fontos a szabályozási paraméter hangolása a legtöbb esetben a releváns jellemzők észleléséhez.

Használjon ötszörös keresztellenőrzést a funkciók kiválasztásának hangolásához az fscnca használatával. A hangolás azt az értéket jelenti, amely a minimális osztályozási veszteséget eredményezi. Hangolás keresztellenőrzéssel:

1. Ossza fel az adatokat öt hajtásra. Minden hajtásnál a cvpartition az adatok négyötödét képzési készletként, az adatok ötödét pedig tesztkészletként rendeli hozzá. Ismét minden egyes hajtáshoz a cvpartition létrehoz egy rétegzett partíciót, ahol minden partíció nagyjából azonos osztályrészekkel rendelkezik.

2. Vonatozza a szomszédsági komponens-elemzés (nca) modelljét az egyes értékekhez az egyes hajtásokban megadott edzéskészlet segítségével.

3. Az nca modell segítségével számítsa ki a hajtás megfelelő tesztkészletének osztályozási veszteségét. Jegyezze fel a veszteség értékét.

4. Ismételje meg ezt a folyamatot az összes hajtás és érték esetén.

Ábrázolja a redők átlagos veszteségértékeit az értékekkel szemben. Ha a minimális veszteségnek megfelelő érték a tesztelt értékek határára esik, akkor az értéktartományt felül kell vizsgálni.

Keresse meg azt az értéket, amely megfelel a minimális átlagos veszteségnek.

Illessze az NCA modellt az összes adathoz a legjobb érték felhasználásával. Használja az LBFGS megoldót, és jelenítse meg a konvergencia információkat.

Ábrázolja a jellemző súlyokat.

Az fscnca helyesen találja ki, hogy az első két jellemző releváns, a többi pedig nem. Az első két jellemző nem egyénileg informatív, de együttesen pontos osztályozási modellt eredményez.

Jósolja meg az osztályokat az új modell használatával, és számítsa ki a pontosságot.

A zavaros mátrix azt mutatja, hogy a –1 osztály előrejelzési pontossága javult. A –1 osztály adatainak 88 előrejelzése szerint –1, 12 közülük az 1. osztályra számítanak. Az 1. osztályból származó adatok 92 előrejelzése szerint az 1. osztályba tartoznak, és közülük 8 előrejelzés szerint osztályból –1.

[1] Yang, W., K. Wang, W. Zuo. "A szomszédsági alkatrészek jellemzőinek kiválasztása nagydimenziós adatokhoz." Journal of Computers. Vol. 7, 1. szám, 2012. január.