Hangolható kölcsönhatásban lévő kompozit fermionfázisok félig töltött kétrétegű-grafén Landau-szinten

Tárgyak

Absztrakt

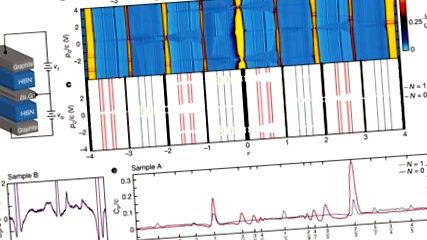
Itt a BLG-készülékek új generációjának magnetokapacitási méréseiről számolunk be, amelyeket az 1a. Ábra vázlatosan ábrázolt. A korábbi kettős kapuzású 13,14,15 eszközarchitektúrákkal ellentétben a kapuelektródák a BLG mindkét oldalán kevés rétegű grafitpelyhekből készülnek, ami jelentősen csökkenti a minta rendellenességét (lásd 11. kiegészítő ábra). A két alkalmazott kapufeszültség összege és különbsége, n0 és o0 (lásd 1. ábra), szabályozza a töltés sűrűségét n és a réteg polarizációs sűrűsége o a kétrétegen belül. Az 1b. Ábra a behatolási mező kapacitását mutatja CP, amely szorosan kapcsolódik a 16 termodinamikai összenyomhatósághoz, a n0–o0 a ZLL-t átfogó sík, −4 1. ábra: Frakcionális kvantum Hall (FQH) effektus minden van der Waals heteroszerkezetben.

Először a páros nevező FQH állapotokat vitatjuk meg. Összenyomhatatlan FQH állapotban véges energiára van szükség egy elektron vagy lyuk injektálásához. Ez a „termodinamikai” rés 16 alapján határozható meg CP, amelyet a 2a. Ábra mutat be különböző hőmérsékleteknél B = 14 T. Ezt a termodinamikai rést az inverz elektronikus összenyomhatóság ∂ integrálásával mérjükμ/ ∂n vonatkozóan n (2b. Ábra), amely 4 K hézagot eredményez a hígító hűtőszekrényünk alaphőmérsékletén (lásd a Kiegészítő információkat). A második eszközről érkező transzportmérések a várható kvantált Hall-fennsíkot és az ezzel járó hosszanti ellenállás minimumát mutatják (2c. Ábra). A hőmérsékletfüggő transzport az aktivációs rés alacsonyabb értékét mutatja, 1,8 ± 0,2 K hőmérsékleten B = 14 T. Ez az eltérés nem meglepő 16. A termodinamikai rés azt az energiát méri, amely egy teljes elektron – lyuk pár hozzáadásához szükséges, míg a termikusan aktivált transzport a frakcionáltan feltöltött kvázirészecske – kvasihole pár injektálásának energiaköltségét méri. Félig kitöltött FQH állapot esetén a kvázirészecske töltése várható e/ 4, ebben az esetben a mért aktivációs résnek nagyjából a 16-os termodinamikai rés egynegyedének kell lennie T = 0.

A kétrétegű elektronrendszerben természetes azt kérdezni, hogy a féltöltésnél megfigyelhető összenyomhatatlan állapotok egy- vagy többkomponensű fázisok-e. Míg az egykomponensű páros nevező FQH fázis vezető elméleti jelöltjei - a párosított Pfaffian 5 és anti-Pfaffian 17,18 államok - nem abeliak, a többkomponensű rendszerekben az abeli „331” fázis valószínűbb 19. A 15 vegyértékpolarizáció térképét felhasználva (amelynek aspektusait itt megismételtük nagyobb felbontásban; lásd: Kiegészítő információk), azt tapasztaljuk, hogy a réses fázis olyan régiókban jelenik meg, ahol a frakcionális kitöltés egyetlen egységbe polarizálódik N = 1 komponens. A helyzet tehát nagyjából hasonló a v = GaAs 5/2 állapota (2. hivatkozás), amelyben a numerikus számok régóta jósolnak páros fázist. Megjegyezzük azonban, hogy a mért aktivációs rés többszörösen nagyobb, mint a GaAs-ban (558 mK; ref. 20), ZnO (90 mK; ref. 4) vagy a felfüggesztett BLG-ben (600 mK; ref. 3) mért legnagyobb rések.

Eredményeink azt sugallják, hogy a kapszulázott BLG bizonyos előnyökkel rendelkezik a GaAs-mal szemben, mint a nem abeli kvarészecskék 11 interferometrikus kimutatásának platformja. Először is, a nagy energiahézag és a GaAs-hoz viszonyított kicsi korrelációs hosszúság csökkentheti a tömeg-él összekapcsolódást, amely káros a 27 interferometrikus szondákra, miközben exponenciálisan elnyomja a hővel aktivált kvázrészecskék sűrűségét. Másodszor, a hatszögletű bór-nitrid kapu dielektrikumai szinte önkényesen vékonyak lehetnek, lehetővé téve az élek és a kvantumpont érintkezők éles elektrosztatikus potenciálok felhasználásával történő kialakítását. A legújabb kísérletek hosszú koherenciahosszakat mutattak a kvantum Hall-rezsimben az ilyen kapu által meghatározott élek mentén 28. Végül a feltételezett pfaffi állam a v = −1/2 a BLG-ben kevesebb élmóddal rendelkezik, mint az anti-Pfaffian állam v = 5/2 GaAs-ban, így az előbbi az interferometria szempontjából előnyösebb jelölt. Fázis-koherens transzportmérések nélkül is, az itt bemutatott, alacsonyabb hőmérsékletekre végzett termodinamikai mérések felhasználhatók a topológiai alapállapot-degeneráció vizsgálatára 29, amelyek egyértelmű bizonyítékot szolgáltathatnak a közeljövőben a nem abeli statisztikákra.

Az adatok elérhetősége

A vizsgálat eredményeit alátámasztó adatok ésszerű kérésre a megfelelő szerzőtől állnak rendelkezésre.

Hivatkozások

Kitaev, A. Yu. Hibatűrő kvantumszámítás bármelyik által. Ann. Phys. 303, 2–30 (2003)

Willett, R. és mtsai. Páros nevező kvantumszám megfigyelése a frakcionált kvantum Hall-effektusban. Phys. Tiszteletes Lett. 59, 1776–1779 (1987)

Ki, D.-K., Fal’ko, V. I., Abanin, D. A. & Morpurgo, A. F. Még a nevező frakcionális kvantum Hall-effektusának megfigyelése szuszpendált kétrétegű grafénban. Nano Lett. 14, 2135–2139 (2014)

Falson, J. és mtsai. Páros nevű frakcionált kvantum Hall-fizika a ZnO-ban. Nat. Phys. 11., 347–351 (2015)

Moore, G. & Read, N. Nonabelions a frakcionált kvantum Hall-effektusban. Nucl. Phys. B 360, 362–396 (1991)

Jain, J. K. Kompozit-fermion megközelítés a frakcionált kvantum Hall-effektushoz. Phys. Tiszteletes Lett. 63, 199–202 (1989)

Halperin, B. I., Lee, P. A. & Read, N. A félig kitöltött Landau-szint elmélete. Phys. Rev. B 47, 7312–7343 (1993)

Willett, R. L., Ruel, R. R., West, K. W. & Pfeiffer, L. N. Fermi felület kísérleti bemutatása a legalacsonyabb Landau-szint felének kitöltésével. Phys. Tiszteletes Lett. 71., 3846–3849 (1993)

Kang, W., Stormer, H. L., Pfeiffer, L. N., Baldwin, K. W. & West, K. W. Mennyire valóságosak az összetett fermionok? Phys. Tiszteletes Lett. 71., 3850–3853 (1993)

Read, N. & Green, D. A fermionok párosított állapota két dimenzióban, a paritás és az idő-megfordulás szimmetriájának megtörésével, valamint a frakcionált kvantum Hall-effektussal. Phys. Rev. B 61, 10267–10297 (2000)

Nayak, C., Simon, S. H., Stern, A., Freedman, M. & Das Sarma, S. nem abeli anionok és topológiai kvantumszámítás. Rev. Mod. Phys. 80, 1083–1159 (2008)

Papic´, Z. & Abanin, D. A. topológiai fázisok a kétrétegű grafén zeroth Landau-szintjén. Phys. Tiszteletes Lett. 112, 046602 (2014)

Lee, K. és mtsai. Kémiai potenciál és kvantum Hall ferromágnesesség kétrétegű grafénben. Tudomány 345, 58–61 (2014)

Maher, P. és mtsai. Hangolható frakcionális kvantum Hall-fázisok kétrétegű grafénben. Tudomány 345, 61–64 (2014)

Hunt, B. M. és mtsai. Diszkrét völgy- és pályakvantumszámok közvetlen mérése kétrétegű grafénben. Nat. Commun. (a sajtóban)

Eisenstein, J. P., Pfeiffer, L. N. & West, K. W. A kétdimenziós elektrongáz összenyomhatósága: a nullterű csereenergia és a frakcionált kvantum Hall-rés mérései. Phys. Rev. B 50, 1760–1778 (1994)

Levin, M., Halperin, B. I. & Rosenow, B. Részecske-lyuk szimmetria és a Pfaff-állapot. Phys. Tiszteletes Lett. 99, 236806 (2007)

Lee, S.-S., Ryu, S., Nayak, C. & Fisher, M. P. A. részecske-lyuk szimmetria és a v = 5/2 kvantum Hall-állapot. Phys. Tiszteletes Lett. 99, 236807 (2007)

Halperin, B. I. A kvantált Hall-vezetőképesség elmélete. Helv. Phys. Acta 56, 75–102 (1983)

Kumar, A., Csáthy, G. A., Manfra, M. J., Pfeiffer, L. N. & West, K. W. Nem konvencionális páratlan nevező frakcionális kvantum Hall-állapotok a második Landau-szinten. Phys. Tiszteletes Lett. 105, 246808 (2010)

Apalkov, V. M. és Chakraborty, T. Stabil Pfaff-állapot kétrétegű grafénban. Phys. Tiszteletes Lett. 107., 186803 (2011)

Metlitski, M. A., Mross, D. F., Sachdev, S. & Senthil, T. Cooper párosítása nem Fermi folyadékokban. Phys. Rev. B 91., 115111 (2015)

Rezayi, H. R. & Simon, S. H. A részecske-lyuk szimmetria megtörése Landau-szintű keveréssel a v = 5/2 kvantált Hall állam. Phys. Tiszteletes Lett. 106., 116801 (2011)

Zaletel, M. P., Mong, R. S. K., Pollmann, F. & Rezayi, E. H. Végtelen sűrűségű mátrix renormalizációs csoport többkomponensű kvantum Hall rendszerek számára. Phys. Rev. B 91., 045115 (2015)

Rezayi, E. H. Landau szintkeveredése és a v = 5/2 kvantum Hall-effektus. Phys. Tiszteletes Lett. 119, 026801 (2017)

Levin, M. & Halperin, B. I. Nem abeli kvázirészecskék kollektív állapotai mágneses mezőben. Phys. Rev. B 79, 205301 (2009)

von Keyserlingk, C. W., Simon, S. H. és Rosenow, B. Enhanced bulk-edge Coulomb coupling in frakcionált Fabry – Perot interferométerek. Phys. Tiszteletes Lett. 115, 126807 (2015)

Wei, D. S. Mach – Zehnder interferometria spin- és völgypolarizált kvantum Hall élállapotok felhasználásával grafénban. Sci. Adv. 3, e1700600 (2017)

Cooper, N. R. & Stern, A. A nem abeli kvantumcsarnok-államok megfigyelhető tömeges aláírásai. Phys. Tiszteletes Lett. 102, 176807 (2009)

Barkeshli, M., Nayak, C., Papic, Z., Young, A. és Zaletel, M. frakcionált exciton Fermi felületek és kondenzátumok kétkomponensű, kvantált Hall állapotban. Preprint: https://arxiv.org/abs/1611.01171 (2016)

Köszönetnyilvánítás

Elismerjük B. Odegard és J. Island kísérleti segítségét, és megbeszéléseket folytattunk M. Barkeshlivel, C. Dean-nal, E.-A. Kim, R. Mong, C. Nayak, Z. Papic, S. Simon és A. Stern. A magnetokapacitási méréseket az NSF finanszírozta a DMR-1636607 alatt. A nanagyártás és a szállítási mérések egy részét az ARO finanszírozta a 69188PHH javaslat alapján. A.F.Y. elismeri a David és Lucile Packard Alapítvány támogatását. A 14 T feletti méréseket a National High Magnetic Field Laboratory-ban végezték, amelyet a National Science Foundation DMR-1157490 számú kooperatív megállapodása és Florida állam támogat. A numerikus szimulációkat a Princeton Institute for Computational Science and Engineering (PICSciE) által támogatott számítási erőforrásokon hajtották végre. E.M.S. elismeri az Elings Fellowship támogatását. K.W. és T. T. elismerik az Elemental Strategy Initiative támogatását, amelyet a MEXT, Japán és a JSPS KAKENHI JP15K21722 támogatási szám vezetett.

Szerzői információk

Hovatartozások

Fizikai Tanszék, Kaliforniai Egyetem, Santa Barbara, 93106, Kalifornia, USA

A. A. Zibrov, C. Kometter, H. Zhou és A. F. Young

California Nanosystems Institute, Kaliforniai Egyetem, Santa Barbara, Santa Barbara, 93106, Kalifornia, USA

Haladó Anyaglabor, Nemzeti Anyagtudományi Intézet, Tsukuba, 305-0044, Ibaraki, Japán

T. Taniguchi és K. Watanabe

Fizikai Tanszék, Princetoni Egyetem, Princeton, 08544, New Jersey, USA

A PubMed Google Scholar alkalmazásban is kereshet erre a szerzőre

Hozzájárulások

A.A.Z., E.M.S. és H.Z. gyártott eszközök A, B, illetve C. T. T. és K. W. szintetizálta a hatszögletű bór-nitrid kristályokat. A.F.Y. és C.K. felépítette a mérõelektronikát. A.A.Z., H.Z., E.M.S. és A.F.Y. megszerezte és elemezte a kísérleti adatokat. M.P.Z. elvégezte a DMRG számításokat. A.A.Z., M.P.Z. és A.F.Y. írta a lap.

Levelezési cím

Etikai nyilatkozatok

Versenyző érdekek

A szerzők kijelentik, hogy nincsenek versengő pénzügyi érdekeik.

További információ

Véleményezői információk Természet köszönet D. Abaninnak, K. Parknak, K. Yang-nak és a többi névtelen bíráló (k) nak a munka szakértői értékeléséhez való hozzájárulásukért.

Kiadói megjegyzés: A Springer Nature semleges marad a közzétett térképeken és az intézményi kapcsolatokban szereplő joghatósági állítások tekintetében.

Kiegészítő információk

Ez a fájl az S1-S17 ábrákat és az S1-S3 táblákat tartalmazza. (PDF 27030 kb)