Kevesebbet mérlegel, ha a Hold felettetek van?

Az univerzumban mindennek, aminek van tömege, van gravitációja. Könnyű megérteni, hogy a Földnek, bármekkora is, van gravitációs képessége, amely folyamatosan ránk húz, és a terra firma-ban tart minket. В Ugyanolyan könnyű megérteni, hogy más nagy objektumok is rendelkeznek gravitációval, mint például a Hold, a bolygók és a Nap.

Sokkal nehezebb megérteni, hogy a Földön minden embernek van gravitációja.В Furcsa módon erőt fejt ki a Földre és minden más emberre. В erőt is kifejtesz minden sziklán, fán és teremtményen, amely a Földet bejárja, és ezek mind erőt gyakorolnak rád. В Az egyetlen probléma az, hogy ilyen kicsi a tömeged a Földhöz képest, az általad kifejtett gravitációs erő nagyon kicsi.

Amikor elmagyarázom ezt az ötletet, gyakran kérdezik tőlem: "Miért nem érezzük a gravitációt egy hegyről?"

Egyrészt azért, mert maga a Föld sokkal többet nyom, mint a hegy, ezért a hegynek alig van gravitációs képessége, annak ellenére, hogy hatalmas. В A másik ok az, hogy bármely gömb eloszlású tömeg (például a Föld) által kifejtett gravitáció úgy viselkedik, mintha az egész tömeg az objektum középpontjában lenne .В Ha szeretné látni a tényleges matematikát, ellenőrizze ezt a linket a bontás.

Ha egy hegy nem tud elegendő erőt kifejteni ahhoz, hogy érezzük, mi van a Holddal? A Hold nagy, és viszonylag közel áll hozzánk. Mi van, ha a Hold fent van? A húzóerő könnyebbé tesz minket? Vajon megnehezítene-e minket, ha a Föld túlsó oldalán lenne?

Találjuk ki!

Isaac Newton először kitalálta a gravitáció erejét és működését. В kidolgozott egy egyenletet a két objektum közötti gravitációs erő mérésére:

Hitel: Wikipedia CC 3.0: Dennis Nilsson

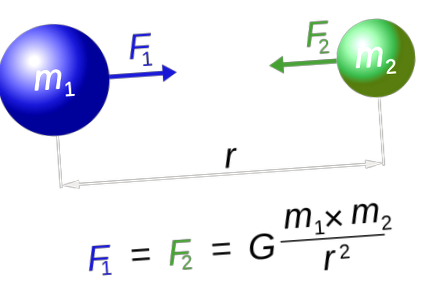
Ahol r az objektumok tömegközéppontja közötti távolság, és G az univerzális gravitációs állandó, ahol G = 6,67 x 10 -11 N (m/kg) 2 .

Te, a Földön állsz!

A Föld súlya 5,72 × 10 24 Kg, és a távolság közted és a Föld közepe között (ahol érzed a gravitáció húzását) r = 6 371 000 m. В Dobja mindezt a fenti egyenletbe, és megállapíthatjuk, hogy a Földről rád gyakorolt erő:

Tömegének 9,4-szerese. В ezért a tömegesebb dolgokat nehezebb felemelni. A tényleges válasz, kiváló minőségű kísérletek alapján, a tömegének 9,81-szerese. В különbözik a számításunktól, annak a ténynek köszönhető, hogy a Föld sűrűsége nem mindenhol ugyanaz (némelyik víz, kőzet stb.). Ha ezt az erőt elosztja a tömegével, akkor a gravitáció miatt megkapja a Föld gyorsulását, függetlenül a tömegtől:

Minden dolog ugyanolyan ütemben gyorsul, bármilyen nehéz is. В A toll olyan gyorsan zuhan, mint egy tekegolyó. Az egyetlen különbség az, hogy a bowlinggolyó sokkal jobban fog fájni, ha rád esik.В

Most a Hold

A Föld és a Hold egy pont körül kering, tömegközéppontjuk. В Mivel a Föld masszívabb, a Föld-Hold rendszer tömegközéppontja a Föld belsejében található, körülbelül 1700 km-rel a felszín alatt. В Ez azt jelenti, hogy a Föld „billeg”, amikor a Hold kering.

Kép jóváírás: Rnt20 Wikipedia CC 3.0

A Föld és a Hold valójában szabad zuhanásban van a tömegközép körül. В Ez megegyezik az űrhajósokkal a Föld körül keringő űrhajóban. В egy ellipszisben zuhannak a Föld körül, de anélkül, hogy egy álló felületet rájuk tolnának, súlytalannak érzik magukat .В Nettó erejük a centripetális erő, amely megegyezik a gravitációs erővel. В A centripetális erőt a következők adják:

Te és a Föld is szabadon esnek a tömegközép körül. В De mivel a Földön állva vagy, a föld rád nyomul, és érzékeled a Föld gravitációját.

"De azt gondoltam, hogy az óceán árapálya a Hold gravitációja miatt következik be!"

Csinálják! Amikor két nagy test kölcsönhatásáról beszélünk, például a Hold gravitációs hatásáról a Földre, meg kell beszélnünk az árapályerőt.

Mivel a Föld nagy szilárd test, teljes tömege azonos sebességgel kering. В Ez az árapályerő kulcsa. A Föld centripetális ereje teljes átmérőjén megegyezik, de mivel a gravitáció a távolságtól függ, a Föld Hold felé eső oldala nagyobb gravitációt érez, mint az oldala. В Ennek eredményeként az árapályerő a Föld mindkét oldalán a középponttól távolabbra mutat.

Ez azt jelenti, hogyВ kevesebbet mérsz, ha a Hold feletted van ÉS amikor a Hold a Föld veled ellentétes oldalán van. В Mindkét esetben a súlya (majdnem) ugyanannyival változik. В Itt található az árapályerő térképe a Föld felszínének különböző pontjairól.

Hitel: Ethan Siegel http://scienceblogs.com/startswithabang

Tehát mennyire erős az árapályerő? Mennyit változik a súlyunk a Hold miatt?

(Megjegyzés: Ha nem szeretné látni a matematikát, görgessen lefelé a válasz megtekintéséhez)

A holdból származó árapályerő megtalálásához összehasonlítjuk a Hold gravitáció miatt bekövetkező Hold gyorsulását a Föld szélén, a Föld középpontjában lévő gyorsulással. В Mivel kapcsolatban vagyunk a Földdel, pontosan ugyanolyan centripetális erővel rendelkezünk, és ezért éreznünk kell a ránk ható árapály erőt is.

A Hold felőli oldalon:

Mivel az Erő = Tömeg x Gyorsulás, felülről vehetjük Newton gravitációs törvényét, és mindkét oldalt eloszthatjuk tömeggel, hogy a következő képletet kapjuk a gyorsuláshoz a gravitáció miatt.

aВ = G * В MВ/r 2

Ebben az esetben a Föld széle esetében r lesz a Föld-Hold távolság (amelyet a Föld közepétől a Hold közepéig mérnek), levonva a Föld sugarát. В Ha elvégezzük a számítást a túloldalra, hozzáadjuk a Föld sugarát a Föld – Hold távolsághoz.

Tehát, ha a Föld-Hold távolság R, és a Föld sugara rEarth,

anearВ = G * В Hónap/(R - r Föld) 2 - G * H Hónap/R 2

A Föld-Hold távolság nagyjából 380 000 000 m, a Föld sugara 6 371 000 m, G = G = 6,67 x 10 -11 N (m/kg) 2, a Hold tömege 7,348 x 10 22 Kg. В A számítás:

anearВ = 0,00000117 m/s 2

Nagyon apró gyorsulás.

A Holddal szemközti oldalon:

A Föld szélére ezúttal r lesz a Föld – Hold távolság plusz a Föld sugara .В Ugyanazon egyenletet használva, mint legutóbb az új távolságokkal, és levonva a szélén lévő gravitációt a középponttól:

messze = G * В Hónap/R 2 – G G * H Hónap/(R + r Föld) 2

Ugyanazokkal a számokkal, mint korábban, a számítás megadja:

távol = 0.00000111 m/s 2

Kissé ónosabb gyorsulás.

Tehát az árapály erő kissé erősebb a Hold felé néző oldalon, de csak körülbelül 5% -kal. Most hasonlítsuk össze ezt a gravitáció miatti gyorsulással a Földön felülről, 9,81 m/s 2 .

A gravitáció, amelyet a Holdról érez, alig több, mint a Földről érzett gravitáció 1 milliomod része, ami azt jelenti, hogy ha a Hold a feje fölött vagy a Föld ellenkező oldalán van, akkor a súlya csak egy millimilliárddal csökken.

Most már teljesen nyilvánvaló, hogy a Hold gravitációja a legkisebb észrevehető hatást sem fogja elérni, és mivel a Nap és más bolygók sokkal távolabb vannak, hatásuk is csekély. В A Naprendszer gravitációja csak nem hat ránk, mert a gravitáció a távolság négyzetével csökken. Valami, ami kétszer olyan messze van a Földtől, csak a gravitáció 1/4-ét érzi. Szóval halasszuk fel egy kicsit. В Van-e olyan hely a Naprendszerben, ahol különbséget észlelnénk?

Ehhez a Jupiter Hold Io-jába utazunk. В Io a legközelebb a galileai holdak közül, a Jupiter pedig a Naprendszer legnagyobb tömegű bolygója. В Más eredményt kapunk?

Az árapályerő ismét könnyebbé tesz minket, ha a Jupiter a feje fölött vagy az ellenkező oldalon áll, akárcsak a Föld és a Hold esetében, de észrevehető különbséget fog-e tenni?

A Jupiter, a Naprendszer legnagyobb bolygójának és az Io, a legközelebbi Hold használatával a Jupiter árapályai könnyebbé tesznek minket?

Ugyanazt az egyenletet fogjuk használni, mint korábban, mivel Newton gravitációs és árapálytörvénye az univerzum nagyjából mindenre vonatkozik (kivéve talán azokat az őrült dolgokat, mint a fekete lyukak).

Ezúttal a tömegek különböznek, csakúgy, mint a távolságok. В Meg fogjuk vizsgálni, hogy mennyit nyomunk az Io-val, és mekkora az árapályerő. В Kezdje a szükséges általános információkkal:

Az Io tömege = 8,93 x 10 22 kg

A Jupiter tömege = 1,898 x 10 27 В kg

Io sugár = 1.821.600 m

Jupiter-Io távolság (középponttól középpontig) = R = 421 700 000 m

1. Gyorsulás a gravitáció miattВ az Io-n

Felejtsük el egy pillanatra a Jupitert, és nézzük meg, mi az Io-n a gravitáció miatti gyorsulás:

Az Io sugárának és tömegének felülről történő felhasználása:

Az Io-nak sokkal kisebb a gravitációja, mint a Földnek, mivel sokkal kisebb. A testsúlyod körülbelül 1/6-át nyomnád a Földön (hasonlóan a Holdhoz).

2. Árapályerő a Jupiter gravitációja miatt

Ismét az Io közeli és távoli oldalára fogunk nézni, ugyanúgy, mint amikor a Földön álltunk. Csak ezúttal hatalmas Jupiter készíti az árapályokat.

A Jupiter felettünk álló oldalra:

Ugyanúgy, mint a Föld és a Hold esetében, meg kell találnunk a különbséget a szélén lévő gravitáció és a középpontban lévő gravitáció között, ezért használjuk:

anearВ = G * В MJupВ/(R - r Io) 2 В - G * В MJupВ/R 2

Ahol R az Io és a Jupiter közötti távolság. В A számítás során a következőket kapjuk:

anearВ = 0,0062 В m/s 2

A Jupiterrel szemközti oldalon:

Ezúttal, mint korábban, hozzáadjuk az Io sugarát a Jupiter-Io távolsághoz, hogy megkapjuk az árapályok helyes mértékét:

messze = G * В MJupВ/R 2 В - G * В MJupВ/(R + r Io) 2

Ahol R az Io és a Jupiter közötti távolság. В A számítás során a következőket kapjuk:

anearВ = 0,0061 В m/s 2

Nagyon érdekes eredmény!

Ez azt jelenti, hogy még a Jupiter erőteljes gravitációja mellett is, az Io-nkénti súlya csak egy tízezer kilogrammal változik!

Az árapályerő ugyanis valóban a tárgyak közötti távolságtól függ. В Ahogy a tárgyak közelebb kerülnek egymáshoz, az árapályerő jelentősen megnő! Ha a Hold kétszer olyan közel lenne hozzánk, mint most, akkor a Földre gyakorolt árapályerők 8-szorosára nőnének!

Még az Io-n is, a Jupiter hatalmas gravitációjával az árapály kicsi, mert az Io elég messze van. Ha az árapályok sokkal erősebbek lennének, a Jupiter könnyedén széthúzta volna az Io-t. В A műhold sértetlenségének minimális távolságát roche-határnak nevezzük. В E pont után az árapályerő nagyobb, mint a műhold saját gravitációja, és széthúzódik.

Maga az Io vulkanikus világ az árapályerők miatt, de ez nem teljesen a Jupiter hibája. В A Jupiter többi galileai holdja hozzájárul ahhoz, hogy az Io különc pályával rendelkezzen, ami az Io keringési távolságának változását okozza. В Ez a Jupiter által érzett árapály erőváltozatait hozza létre, és az árapályok váltakozása következtében Io kérge rendszeresen lökődik és húzódik, súrlódást hoz létre a kéregben és hatalmas mennyiségű hő keletkezik, amely vulkáni tevékenységként nyilvánul meg.

Ennél nem sokkal őrültebb. Â Külön köszönöm Jesse Rogersonnak, hogy kétszer is ellenőrizte a matekomat. В Köszönjük, hogy elolvasta! Soha ne felejtsd el, milyen csodálatos és őrült és félelmetes lehet az Univerzum!

25 gondolat: „Kevesebbet mérlegelsz, amikor a Hold feletted van? ”

Nagyon érdekes! Köszönöm

Ne hagyja, hogy a Súlyfigyelők elkapják ezt a szelet.

igazán nagyszerű magyarázat és cikk. További jó munkát

Nagyon szépen köszönöm! Kérjen bátran minden olyan témát, amelyet szeretne megtekinteni!

Azt hiszem, rossz szót használtál. A Centripedalnak centrifugálisnak kellett volna lennie. Ha a személy ereje középpontú lenne, az nem "ellensúlyozná" a gravitációs erőt, akkor működne vele.
Kérjük, tudassa velem, hogy helyes-e ebben a kérdésben.
Thanx
Harold

Köszönöm a megjegyzést Harold. Elgondolkodtattál rajta, és egy ideig mélyebbre ástam, hogy megpróbáljam rendezni az egészet. Kiderül (sajnos), hogy mindketten tévedünk.

Először: Centripetal vs. Centrifugal. A hasonlat, amelyet használni fogok, egy yo-yo lendült a fejed körül. A jo-yo lengésével fontos szempont, hogy nettó erő hatjon rá, mivel az irányváltással gyorsul. Ez a nettó erő a centripetális erő, és egyenlő a kötél feszültségével. Ha nem lenne ott, akkor a jo-jo már nem maradna körkörös mozgásban, hanem egyenes vonalban repülne el. A tárgynak a körmozgásra való hajlamát néha centrifugális erőnek nevezik, de ez nem valós erő. Ehelyett az objektum tehetetlensége okozza ezt az egyenes tendenciát. Az egyetlen valódi erő, amely a jo-jo-ra hat, a kötél feszültségéből fakadó centripetális erő.

Most az űrben meg kell különböztetnünk a kontaktus és az érintés nélküli erőket. A kontakt erők, amelyeket néha normál erőknek is neveznek, mindig hatnak ránk a Földön. Leülve érezzük, hogy a szék felfelé tolódik, ellenáll a gravitációnak. Nem igazán érezzük a gravitációt, érezzük, hogy a talaj kontaktusereje ránk nyomul, ellenáll a gravitációs erőnek.

Most itt tévedtem. A szabad esést és a súlytalanságot nulla nettó erővel társítottam. A pályán lévő űrhajós gyorsul, kell, hogy legyen, mozgásuk iránya folyamatosan változik, amikor elliptikus pályán mozognak a Föld körül. Tehát van egy nettó erejük, amely a centripetális erő, és egyben a gravitációs erő is, ebben az esetben egy és ugyanaz, mint a jo-jo hasonlat feszültsége esetén. De nincsenek kontakt erők, semmi nem nyomja őket, ami lehetővé teszi számukra a gravitációs erő érzését. Ez az, ami a szabadesés. Ez nem a gravitáció hiánya, hanem a kontakt erők hiánya. Ez Einstein cselekvésbeli relativitása.

Még egy megfontolandó szempont ennek magyarázatához. Ha egy liftben lennék, amely a Föld felé zuhan, akkor a liften kívül nem látok semmit, ezért súlytalannak érzem magam, és lebeghetek a liftben. A gravitáció továbbra is hatással van rám és a liftre, de nincsenek érintkezési erők a földtől, vagy bármi más.

Remélem, ennek van értelme, és köszönöm a megjegyzését! Megváltoztatom a bejegyzést, hogy tisztázzam az eredeti magyarázatom zavart.

Gondolom, úgy gondolhatna az űrhajósokra, hogy „szabad esésben” vannak, de szerintem ez inkább olyan, mint egy egyensúlyi állapot.
A „szabad zuhanás” pontosabb lenne egy olyan tárgy leírására, amely 0 mérföld/órás sebességgel halad, összehasonlítva a föld felszínével (a gravitáció húzóerejét érintve), ezért azonnal szabadon gyorsul a föld felé, centrifugális erők nélkül harci gravitáció.
Az űrhajósok viszont nagy sebességgel haladnak, érintve a föld gravitációját. Ha ezt a sebességet megnövelik, akkor „kiszöknek” a föld gravitációjából és lőnek az űrbe ... ha ez a sebesség csökken, akkor leereszkednek a föld légkörébe, ahol a légköri súrlódás miatt gyorsan lelassulnak, és a föld felszínére égnek.
Összegzés: az űrhajósok nincsenek szabad zuhanásban - lehet, hogy leesnek -, de a legfontosabb erő, amely stabilan tartja őket, az az energia, amely felgyorsította őket pályapályájuk sebességére, valamint a lassításukhoz szükséges semmi hiánya.
Thanx a bejegyzésért és a webhelyért, és mindenért, amit megtesz az emberek oktatása érdekében! ! !
Harold

Köszönöm a megjegyzést Harold - azt hiszem, ez megoldódik a másik megjegyzésedre adott válaszommal. Szívesen megbeszéljük egy kicsit tovább, ha úgy tetszik.

Kérdésem van,

Amikor az űrben mesterséges gravitációt hozhat létre, azáltal, hogy az entitás forog. Az erő rajtad van, amely a lábad felé nyomja, miközben fejeddel a centrifuga közepe felé nézel. De mi lenne, ha a hold a föld körül forogna, és nem forogna. Nem különbözne-e a gravitáció a hold egyik oldalán, mint a föld felé néző oldalon?

Először a Hold forog! De ezt úgy hívjuk, hogy „ártalmasan bezárva” a Földhöz, tehát ugyanolyan idő alatt forog, amennyi a keringéshez szükséges, 29,5 nap. Képzelje el, hogy képzelje el, hogy a Föld kering a Hold körül, fordítva. Ha mindig ugyanazt a Hold arcát látnánk, akkor annak forognia kell, amikor körülötte keringünk.

- Nem különbözne a gravitáció a hold egyik oldalán, mint a föld felé néző oldalon?

Az árapályerő miatt is, kivéve, hogy ezúttal a Föld gyakorolja a Holdra, de ezek az árapályerők megint túl kicsiek ahhoz, hogy különbséget tegyenek egy apró ember számára. Ami a centripetális erőket illeti, a szögsebesség különbsége a Hold közeli és távoli oldala között kicsi, ezért az ebből fakadó centripetális erők eltérése még a cikkben tárgyalt árapályerőnél is vékonyabb.

Mondja meg, ha jól értettem kérdéseit - szívesen válaszolok, ha nyomon követi.

Nagyon köszönöm ezért ... Pontosan ezt kerestem a Google-on, miközben arra gondoltam, vajon könnyebb vagyok-e, amikor a hold fent van.
A magyarázata nagyon alapos volt, és akkor megelőzött egy további kérdést, amikor újra elvégezte a matematikát az Io рџ ?