Archimedes; A határtalan fizika elve
Az objektum felhajtó erejét az Archimédész elv alapján lehet kiszámítani.
Tanulási célok
Számítsa ki a felhajtóerő irányát
Key Takeaways
Főbb pontok
- A felhajtóerőt a folyadék által kifejtett nyomás okozza, amelybe egy tárgyat merítenek.
- A felhajtóerő mindig felfelé mutat, mert a folyadék nyomása a mélységgel növekszik.
- Kiszámíthatja a felhajtóerőt akár közvetlenül az objektum minden felületére gyakorolt erő kiszámításával, akár közvetett módon az elmozdított folyadék súlyának megkeresésével.
Kulcsszavak
- lendületes erő: Felfelé irányuló erő, amelyet egy folyadék fejt ki, amely szembeszáll a merülő tárgy súlyával.
- Archimédész-elv: A folyadékba merített testre gyakorolt felhajtóerő megegyezik a test által kiszorított folyadék súlyával.
Amikor felemelkedik a meleg fürdőben való áztatástól, furcsán nehéznek érezheti karját. Ez a hatás a víz felhajtó erejének elvesztésének tudható be. Mi hozza létre ezt a lendületes erőt? Miért van az, hogy egyes dolgok lebegnek, mások pedig nem? A süllyedő tárgyak kapnak-e egyáltalán támaszt a folyadéktól? Bolygatja-e testét a légkör, vagy csak héliumgömbök érintettek?
Élénk erő: Ok és számítás
A fenti kérdésekre a válaszokat abban találjuk, hogy bármely adott folyadékban a nyomás mélységgel növekszik. Ha egy tárgy folyadékba merül, az objektum alján lévő felfelé irányuló erő nagyobb, mint a tárgy tetején lévő lefelé irányuló erő. Az eredmény nettó felfelé irányuló erő (felhajtó erő) bármely folyadékban lévő bármely tárgyra. Ha a felhajtó erő nagyobb, mint a tárgy súlya, akkor a tárgy felszínre emelkedik és lebeg. Ha a felhajtó erő kisebb, mint a tárgy súlya, a tárgy elsüllyed. Ha a felhajtó erő megegyezik a tárgy súlyával, akkor a tárgy ebben a mélységben felfüggesztve marad. A felhajtó erő mindig jelen van a folyadékban, függetlenül attól, hogy egy tárgy lebeg, süllyed vagy felfüggesztve marad.
A felhajtó erő a folyadék által kifejtett nyomás eredménye. A folyadék egy elmerült tárgy minden oldalán nyomja, de mivel a nyomás a mélységgel növekszik, a nyomás erősebb a tárgy alsó felületén, mint a tetején (ahogyan látható).
Kiszámíthatja az objektumra ható felhajtóerőt úgy, hogy összeadja az objektum összes oldalán kifejtett erőket. Például vegye figyelembe a.
A felső felület területe [latex] \ text [/ latex] és mélységben van [latex] \ text_1 [/ latex]; a nyomás ebben a mélységben:
[latex] \ szöveg
_1 = \ text_1 \ rho \ text [/ latex],
ahol [latex] \ rho [/ latex] a folyadék sűrűsége és [latex] \ szöveg \ kb. 9,81 \, \ mathrm> ^ 2 >> [/ latex] a gravitációs gyorsulás. A felső felületen az erő nagysága:
[latex] \ text_1 = \ text
_1 \ text = \ text_1 \ rho \ text \ text [/ latex].
Ez az erő lefelé mutat. Hasonlóképpen, az alsó felületre gyakorolt erő:
[latex] \ text_2 = \ text
_2 \ text = \ text_2 \ rho \ text \ text [/ latex]
és felfelé mutat. Mivel hengeres, az objektum oldalain lévő nettó erő nulla - a felület különböző részein lévő erők szemben állnak egymással és pontosan eltűnnek. Így a hengerre a folyadék hatására felfelé irányuló nettó erő:
[latex] \ text_ \ text = \ text_2 - \ text_1 = \ rho \ text \ text (\ text_2 - \ text_1) [/ latex]
Archimedes-elv
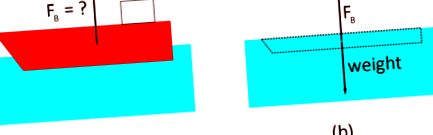
Bár a felhajtóerő ilyen módon történő kiszámítása mindig lehetséges, gyakran nagyon nehéz. Az Archimédész elvéből következik egy egyszerűbb módszer, amely kimondja, hogy a folyadékba merített testre kifejtett felhajtó erő megegyezik a test által kiszorított folyadék tömegével. Más szavakkal, az objektumra ható felhajtó erő kiszámításához feltételezzük, hogy a tárgy merülő része vízből áll, majd kiszámoljuk a víz súlyát (amint látható).
Archimédész-elv: A hajó felhajtó ereje (a) megegyezik a hajó által kiszorított víz tömegével - ab) pontban szaggatott régióként jelenik meg.
Az elvet képletként lehet megfogalmazni:
Az Archimédész-elv mögött az az érvelés áll, hogy az objektum felhajtóereje attól függ, milyen nyomást gyakorol a folyadék az elmerült felületére. Képzelje el, hogy a tárgy merülő részét kicseréljük a folyadékkal, amelyben benne van, amint a (b). A felhajtóerőnek ennek a folyadékmennyiségnek meg kell egyeznie az eredeti tárgy (hajó) hatásával. Ugyanakkor azt is tudjuk, hogy a folyadékra ható felhajtóerőnek meg kell egyeznie a tömegével, mivel a folyadék önmagában nem süllyed el. Ezért az eredeti tárgyra ható felhajtóerő megegyezik a „kiszorított folyadék” súlyával (ebben az esetben a szaggatott tartományban lévő víz (b)).
Az Archimédész-elv minden folyadékra érvényes - nemcsak folyadékokra (például víz), hanem gázokra (például levegő) is. Ezt tovább vizsgáljuk, amikor a következő szakaszokban megvitatjuk az elv alkalmazását.
Archimédész elve - Egyszerű példa: Archimédész elvét használjuk annak meghatározására, hogy mennyi pingvint képes egy jég úszó szárazon támogatni.
Teljes merítés
A felhajtóerő a kötet teljesen elmerült objektumán a [latex] \ text_ \ text = \ text \ rho \ text [/ latex].
Tanulási célok
Azonosítsa azokat a tényezőket, amelyek meghatározzák a felhajtóerőt egy teljesen elmerült objektumon
Key Takeaways
Főbb pontok
- Ha egy tárgy teljesen el van merülve, a kiszorított folyadék térfogata megegyezik az objektum térfogatával.
- A hőlégballonok, a kormányozható eszközök és más tárgyak felhajtóereje kiszámítható azzal a feltételezéssel, hogy azok teljesen el vannak merülve a levegőben.
- A felhajtóerő nem függ a tárgy alakjától, csak annak térfogatától.
Kulcsszavak
- Archimédész-elv: A folyadékba merített testre kifejtett felhajtóerő megegyezik a test által kiszorított folyadék tömegével.
Az Archimédész elv a legkönnyebben érthető és alkalmazható teljesen merülő objektumok esetén. Ebben a részben néhány releváns példát tárgyalunk. Általánosságban elmondható, hogy a teljesen alámerült tárgy felhajtóerejét a képlet adja meg:
[latex] \ text_ \ text = \ text \ rho \ text, [/ latex]
ahol a [latex] \ text [/ latex] az objektum térfogata, [latex] \ rho [/ latex] a folyadék sűrűsége, a [latex] \ text [/ latex] pedig gravitációs gyorsulás. Ez azonnal következik Archimédész elvéből, és az a tény, hogy az objektum teljesen el van merülve (és így a kiszorított folyadék térfogata csak az objektum térfogata).
Henger
Az előző szakaszban kiszámoltuk a henger felhajtóerejét (látható), figyelembe véve a henger mindkét oldalán kifejtett erőt. Most ezt az erőt kiszámítjuk Archimédész elvével. A henger felhajtóereje megegyezik a kiszorított folyadék tömegével. Ez a tömeg megegyezik a kiszorított folyadék tömegével és a gravitációs gyorsítással megszorozva:
Élénk erő: A folyadék a merülő tárgy minden oldalára tolódik. Mivel azonban a nyomás a mélységgel növekszik, az alsó felület (F2) felfelé tolása nagyobb, mint a felső felület lefelé irányuló nyomása (F1). Ezért a nettó felhajtóerő mindig felfelé mutat.
A kiszorított folyadék tömege megegyezik a térfogatának és a sűrűségének szorzatával:
Azonban (és ez a döntő pont), a henger teljesen el van merülve, így a kiszorított folyadék térfogata csak a henger térfogata (lásd), és:
Archimédész-elv: A kiszorított folyadék (b) térfogata megegyezik az eredeti henger térfogatával (a).
A henger térfogata az alapja területe megszorozva a magasságával, vagy esetünkben:
Ezért a henger felhajtóereje:
[latex] \ text_ \ text = \ text_ \ mathrm> \ text = \ text_ \ mathrm> \ rho \ text = (\ text_1 - \ text_2) \ rho \ text \ text [/ latex].
Ez ugyanaz az eredmény, amelyet az előző szakaszban kaptunk, figyelembe véve a folyadék által kifejtett nyomás miatti erőt.
Hélium léghajó
Vegyük figyelembe az USS Macon héliummal töltött léghajót (látható). Borítékja (a „léggömb”) 184 059,5 köbméter héliumot tartalmazott. Figyelmen kívül hagyva a gondola kis térfogatát, mi volt a felhajtóerő ezen a léghajón? Ha a léghajó súlya 108 000 kg volt, mennyi rakományt tudott szállítani? Tegyük fel, hogy a levegő sűrűsége 1,225 kg/köbméter. A léghajó felhajtóereje annak a levegőnek köszönhető, amelyben elmerül. Bár nem ismerjük a léghajó pontos alakját, ismerjük annak térfogatát és a levegő sűrűségét, és így kiszámíthatjuk a felhajtóerőt:
Hélium léghajó: Az 1930-as évek héliummal töltött léghajója a USS Macon.
A léghajó teherbírásának megállapításához levonjuk a léghajó súlyát a felhajtóerőből:
A léghajó által hordozott tömeg:
Flotáció
Egy tárgy lebeg, ha a folyadék által rá kifejtett felhajtóerő kiegyensúlyozza a súlyát.
Tanulási célok
Fejezze ki az úszó tárgy felhajtóereje és súlya közötti kapcsolatot
Key Takeaways
Főbb pontok
- A tárgy által tapasztalt felhajtóerő annak alakjától függ.
- Az objektum térfogatának a töredékét az átlagos sűrűségének és a folyadéknak az aránya adja meg: [latex] \ bar_ \ mathrm>/\ rho_ \ mathrm> [/ latex].
- Egy tárgy lebeg, ha a folyadék által rá kifejtett felhajtóerő kiegyensúlyozza a súlyát.
Kulcsszavak
- Archimédész elv: A folyadékba merített testre kifejtett felhajtóerő megegyezik a test által kiszorított folyadék tömegével.
Miért lebegnek egyes tárgyak, mások viszont nem? Ha egy fémérmét egy pohár vízbe tesz, az elsüllyed. De a legtöbb hajó fémből készül, és lebegnek. Tehát hogyan lehetséges?
Az úszás feltétele
Egy tárgy akkor fog lebegni, ha a folyadék által rá kifejtett felhajtóerő kiegyensúlyozza a súlyát, vagyis ha [latex] \ text_ \ text = \ text [/ latex].
Az archimédészi elv azonban kimondja, hogy a felhajtó erő a kiszorított folyadék súlya. Tehát egy folyadékon úszó tárgy esetében az elmozdított folyadék súlya a tárgy súlya. Így csak a lebegés speciális eseteiben felel meg a tárgyra ható felhajtó erő a tárgy súlyával. Vegyünk egy tonnás szilárd vastömböt. Mivel a vas közel nyolcszor sűrűbb, mint a víz, víz alá merülve csak 1/8 tonna vizet szorít ki, ami nem elegendő a felszínen tartásához. Tegyük fel, hogy ugyanazt a vastömböt egy tálba alakítják át. Súlya még mindig egy tonna, de ha vízbe teszik, akkor nagyobb vízmennyiséget szorít ki, mint amikor tömb volt. Minél mélyebbre merül a vasedény, annál több vizet kiszorít, és annál nagyobb a rá ható felhajtóerő. Ha a felhajtó erő egy tonna, akkor nem süllyed tovább.
Amikor bármely hajó kiszorítja a saját súlyával megegyező víztömeget, akkor lebeg. Ezt gyakran „flotálás elvének” nevezik, amikor egy lebegő tárgy kiszorítja a folyadék saját súlyával megegyező tömegét. Minden hajót, tengeralattjárót és kormányozhatót úgy kell megtervezni, hogy a saját tömegével megegyező folyadéktömeget kiszorítsa. Egy 10 000 tonnás hajót elég szélesre kell építeni ahhoz, hogy 10 000 tonna vizet kiszorítson, mielőtt túl mélyre süllyedne a vízben. Ugyanez vonatkozik a levegőben lévő edényekre is (mivel a levegő folyadék): A 100 tonna súlyú irányítható eszköz legalább 100 tonna levegőt kiszorít; ha többet kiszorít, akkor emelkedik; ha kevesebbet kiszorít, akkor esik. Ha a dirigálható pontosan elmozdítja a súlyát, állandó magasságban lebeg.
Flotáció és sűrűség
Archimedes elvében a sűrűség döntő szerepet játszik. Egy tárgy átlagos sűrűsége az, ami végső soron meghatározza, hogy lebeg-e. Ha átlagos sűrűsége kisebb, mint a környező folyadéké, akkor lebeg. Ennek oka az, hogy a nagyobb sűrűségű folyadék ugyanabban a térfogatban több tömeget és így nagyobb tömeget tartalmaz. A felhajtóerő, amely megegyezik a kiszorított folyadék tömegével, így nagyobb, mint a tárgy súlya. Ugyanígy a folyadéknál sűrűbb tárgy is elsüllyed. Az, hogy az úszó tárgy mennyire merül el, attól függ, hogy az objektum sűrűsége hogyan függ össze a folyadék sűrűségével. Például egy kirakodatlan hajó sűrűsége alacsonyabb, és kevesebb, mint alatta van alámerülve ugyanahhoz a rakományt megrakott hajóhoz képest. A sűrűség figyelembevételével levezethetjük az elmerült frakció kvantitatív kifejezését. Az elmerült frakció az elmerült térfogat és az objektum térfogatának aránya, vagy
Sűrűség és merülés: Terheletlen hajó (a) magasabb szinten úszik a vízben, mint egy megrakott hajó (b).
Az elmerült térfogat megegyezik a kiszorított folyadék térfogatával, amelyet [latex] \ text_ \ mathrm> [/ latex] -nek nevezünk. Most megkaphatjuk a sűrűségek közötti kapcsolatot, ha a kifejezésbe helyettesítjük a [latex] \ rho = \ text \ text [/ latex] szót. Ez ad
ahol [latex] \ bar_ \ mathrm> [/ latex] az objektum átlagos sűrűsége, és [latex] \ rho_ \ mathrm> [/ latex] a folyadék sűrűsége. Mivel az objektum úszik, a tömege és az elmozdított folyadék tömege megegyezik, ezért kilépnek az egyenletből, így távoznak
Pár dolgot érdemes megjegyezni ezzel a kifejezéssel kapcsolatban:
- Vegye figyelembe, hogy megemlíti az objektum átlagos sűrűségét. Ez sokkal kisebb lehet, mint az anyag sűrűsége, amelyből a tárgy készül. Például egy acélhajót valójában többnyire levegő tölt meg (gondoljunk csak a folyosókra, a raktérekre stb.), Tehát átlagos sűrűsége a levegő és az acél között van. Pontosabban: az átlagos sűrűséget úgy definiáljuk, hogy az objektum teljes tömegét elosztjuk annak teljes térfogatával: [latex] \ bar = \ text/\ text [/ latex].
- Ennek a képletnek csak akkor van értelme, ha az objektum sűrűsége kisebb, mint a folyadék sűrűsége. Ellenkező esetben az elmerült frakció nagyobb lesz, mint egy - annak a jele, hogy az objektum egyáltalán nem lebeg, de elsüllyed!
- 011 Miért kell a gyógyításra összpontosítania, nem pedig a fogyásra, hogy egészséges kegyelmet kapjon; Grit
- Almaecet-diéta - Almaecet segít-e lefogyni
- Kerti zöldséglista a fogyáshoz - vidék
- Almaecetes italital recept 4 egyszerű recept
- Egy pohár Borjomi étkezés előtt a fogyás alapelvei; Блог BORJOMI ОК