Osztályozási hiba - MATLAB

L = veszteség (ens, tbl, ResponseVarName)
L = veszteség (ens, tbl, Y)
L = veszteség (ens, X, Y)
L = veszteség (___, név, érték)

Leírás

L = veszteség (ens, tbl, ResponseVarName) a tbl prediktorok táblája és a tbl valós osztálycímkék segítségével kiszámított együttes ens osztályozási hibáját adja eredményül. .

L = veszteség (ens, tbl, Y) a tbl prediktorok táblázata és az Y igazi osztálycímkék segítségével kiszámított együttes ens osztályozási hibáját adja eredményül. .

L = veszteség (ens, X, Y) az X prediktorok mátrixa és az Y valós osztálycímkék segítségével kiszámított együttes ens osztályozási hibáját adja eredményül. .

L = veszteség (___, Név, Érték) kiszámítja az osztályozási hibát egy vagy több Név, Érték pár argumentum által megadott további opciókkal, az előző szintaxisok bármelyikének felhasználásával.

A veszteség kiszámításakor a veszteség normalizálja a ResponseVarName vagy Y osztálybeli valószínűségeit az edzéshez használt osztály valószínűségekkel, az ens Prior tulajdonságában tárolva .

Beviteli érvek

Fitcensemble-rel létrehozott osztályozási együttes, vagy compact-nal létrehozott kompakt osztályozási együttes .

Mintadat, táblázatként megadva. A tbl minden sora egy megfigyelésnek felel meg, és minden oszlop egy prediktor változónak felel meg. A tbl-nek tartalmaznia kell a modell kiképzéséhez használt összes prediktort. Nem engedélyezett többoszlopos változók és cellarendszerek, kivéve a karaktervektorok sejttömbjeit.

Ha egy táblázatban található mintaadatok felhasználásával képezte magát, akkor ennek a módszernek a bemeneti adatainak is táblázatban kell lenniük.

Válaszváltozó neve, a tbl változó neveként megadva .

Meg kell adnia a ResponseVarName karaktervektort vagy karakterlánc skalárt. Például, ha az Y válaszváltozót tbl.Y fájlként tárolja, akkor adja meg azt „Y” -ként. Egyébként a szoftver a tbl összes oszlopát, beleértve az Y-t is, prediktorként kezeli a modell oktatása során.

Osztályozandó adatok mátrixa. Az X minden sora egy megfigyelést és minden oszlop egy prediktort képvisel. Az X-nek ugyanannyi oszlopnak kell lennie, mint az ens edzéséhez használt adatoknak. Az X-nek ugyanannyi sornak kell lennie, mint az Y-ben lévő elemek számának .

Ha egy mátrixban található mintaadatokat használva képezte magát, akkor ennek a módszernek a bemeneti adatainak is mátrixban kell lenniük.

A megfigyelések osztálycímkéi tbl-ben vagy X-ben. Y-nak ugyanolyan típusúnak kell lennie, mint az ens edzéséhez használt osztályozásnak, és elemeinek számának meg kell egyeznie a tbl vagy az X sorok számával .

Név-érték pár érvek

Adjon meg opcionálisan vesszővel elválasztott Név, Érték argumentumokat. A név az argumentum neve, az Érték pedig a megfelelő érték. A névnek idézőjelek között kell szerepelnie. Több név- és értékpár argumentumot megadhat bármilyen sorrendben: Név1, Érték1. Név, ÉrtékN .

A gyengén tanulók mutatói az együttesben 1-től kezdve. a veszteség csak ezeket a tanulókat használja a veszteség kiszámításához.

Alapértelmezett: 1: NumTrained

Veszteségfüggvény, vesszővel elválasztott párként megadva, amely „LossFun” -ból és egy beépített veszteségfüggvény-névből vagy függvényfogantyúból áll.

Az alábbi táblázat az elérhető veszteségfüggvényeket sorolja fel. Adjon meg egyet a megfelelő karakter vektorral vagy karakterlánc skalárral.

ValueDescription

„binodeviance”	Binomiális eltérés
'classsiferror'	Osztályozási hiba
„exponenciális”	Exponenciális
'zsanér'	Zsanér
„logit”	Logisztikai
„mincost”	Minimális várható téves osztályozási költség (a hátsó valószínűségű osztályozási pontszámoknál)
'négyzetes'	Négyzetes

A „mincost” alkalmas az utólagos valószínűségű osztályozási pontszámokra.

A zsákos és az altéres együttesek alapértelmezés szerint visszaadják a hátsó valószínűségeket (a módszer „Bag” vagy „Subspace”).

Ha az együttes módszer 'AdaBoostM1', 'AdaBoostM2', GentleBoost vagy 'LogitBoost', akkor a hátsó valószínűségek osztályozási pontszámként való használatához meg kell adnia a kettős logit pontszám transzformációt a megadásával

Az összes többi együttes módszer esetében a szoftver nem támogatja az utólagos valószínűségeket osztályozási pontszámként.

Adja meg saját funkcióját a függvény fogantyújának jelölésével.

Tegyük fel, hogy n az X-ben megfigyeltek száma, K pedig a különálló osztályok száma (numel (ens.ClNNames), ens az input modell). A funkciójának rendelkeznie kell ezzel az aláírással

A kimeneti argumentum veszteségértéke skalár.

Kiválasztja a függvény nevét (lossfun).

C egy n -by-K logikai mátrix sorokkal, amelyek jelzik, hogy a megfelelő megfigyelés melyik osztályba tartozik. Az oszlopok sorrendje megfelel az ens.ClassNames osztályosztály sorrendjének .

Szerkessze C-t úgy, hogy a C (p, q) = 1 értéket állítja be, ha p megfigyelés a q osztályba tartozik, minden sorhoz. Állítsa a p sor összes többi elemét 0-ra .

S az osztályozási pontszámok n-by-K numerikus mátrixa. Az oszlopok sorrendje megfelel az ens.ClassNames osztályosztály sorrendjének. S az osztályozási pontszámok mátrixa, hasonlóan a jóslás kimenetéhez .

W a megfigyelési súlyok n-by-1 numerikus vektora. Ha elhalad W-n, a szoftver normalizálja őket úgy, hogy összeadják 1-re .

A költség a tévesen besorolt költségek K-k-K numerikus mátrixa. Például a Költség = egyek (K) - szem (K) értéke 0 a helyes osztályozáshoz, 1 pedig a téves osztályozáshoz.

Adja meg a funkcióját a 'LossFun', @ lossfun gombbal .

A veszteségfüggvényekkel kapcsolatban lásd: Osztályozási veszteség.

Alapértelmezett: 'classsiferror'

Az L kimenet jelentése:

„együttes” - az L skaláris érték, az egész együttes vesztesége.

„egyén” - L egy vektor, amelynek képzett tanulónként egy eleme van.

„kumulatív” - L olyan vektor, amelyben J elemet kapunk az 1: J tanulók felhasználásával a tanulók bemeneti listájáról.

Alapértelmezett: 'együttes'

N -by-T méretű logikai mátrix, ahol:

N az X sorainak száma .

T a gyengén tanulók száma az ens-ben .

Ha a UseObsForLearner (i, j) igaz, akkor a j tanulót használjuk az X i. .

Alapértelmezett: igaz (N, T)

Megfigyelési súlyok vektora, nem negatív bejegyzésekkel. A súlyok hosszának meg kell egyeznie az X sorainak számával. Amikor megadja a súlyokat, a veszteség normalizálja a súlyokat, így az egyes osztályok megfigyelési súlyai összeadódnak az adott osztály előzetes valószínűségével.

Alapértelmezett: egyek (méret (X, 1), 1)

Kimeneti érvek

Osztályozási veszteség, alapértelmezés szerint a rosszul osztályozott adatok töredéke. L lehet vektor, és a név-érték pár beállításaitól függően különböző dolgokat jelenthet.

Példák

Becsülje meg az osztályozási hibát

Töltse be Fisher írisz adatkészletét.

Képezzen 100 döntési fából álló osztályozási együttest az AdaBoostM2 segítségével. Gyengén tanulóként adja meg a fatuskókat.

Becsülje meg a modell osztályozási hibáját a képzési megfigyelések segítségével.

Alternatív megoldásként, ha az ens nem kompakt, akkor megbecsülheti az edzésminta besorolási hibáját az ens továbbadásával a resubLoss-nak .

További információ

Osztályozási veszteség

Az osztályozási veszteségfüggvények az osztályozási modellek prediktív pontatlanságát mérik. Ha összehasonlítja az azonos típusú veszteségeket sok modell között, az alacsonyabb veszteség jobb prediktív modellt jelez.

Vegye figyelembe a következő forgatókönyvet.

L az osztályozási veszteség súlyozott átlaga.

n a minta mérete.

Bináris osztályozáshoz:

yj a megfigyelt osztálycímke. A szoftver –1 vagy 1-ként kódolja, jelezve a negatív vagy a pozitív osztályt.

f (Xj) az X előrejelző adatok j megfigyelésének (sor) nyers osztályozási pontszáma.

mj = yj f (Xj) a j megfigyelés osztályozása az yj-nek megfelelő osztályba. Az mj pozitív értékei a helyes osztályozást jelzik, és nem járulnak hozzá sokat az átlagos veszteséghez. Az mj negatív értékei helytelen osztályozást jeleznek, és jelentősen hozzájárulnak az átlagos veszteséghez.

A többosztályos osztályozást támogató algoritmusok (azaz K ≥ 3) esetén:

yj * a K - 1 nullák vektora, ahol 1 az igaz, megfigyelt yj osztálynak megfelelő helyzetben van. Például, ha a második megfigyelés valódi osztálya a harmadik osztály és K = 4, akkor y2 * = [0 0 1 0] ′. Az osztályok sorrendje megfelel a bemeneti modell ClassNames tulajdonságának sorrendjének.

f (Xj) az X előrejelző adatok j megfigyeléséhez tartozó osztályozási pontszámok K hosszúságú vektora. A pontszámok sorrendje megfelel az osztályok sorrendjének a bemeneti modell ClassNames tulajdonságában.

mj = yj * ′ f (Xj). Ezért mj az a skaláris osztályozási pontszám, amelyet a modell megjósol az igaz, megfigyelt osztályra.

A j megfigyelés súlya wj. A szoftver normalizálja a megfigyelési súlyokat úgy, hogy azok összeadódjanak a megfelelő korábbi osztály valószínűséggel. A szoftver normalizálja az előzetes valószínűségeket is, így ezek összege 1-re nő. Ezért,

Ennek a forgatókönyvnek az ismeretében az alábbi táblázat leírja azokat a támogatott veszteségfüggvényeket, amelyeket a 'LossFun' név-érték pár argumentummal határozhat meg.

L = ∑ j = 1 n w j I < y ^ j ≠ y j >.

Az osztályozási hiba a rosszul osztályozott megfigyelések súlyozott hányada, ahol y ^ j a maximális hátsó valószínűségű osztálynak megfelelő osztálycímke. én< x> az indikátor funkció.

A szoftver ezzel az eljárással kiszámítja a súlyozott minimális költségeket a j = 1. n megfigyelésekhez.

Becsülje meg a j megfigyelés várható osztályozási költségeinek 1-by-K vektorát:

γ j = f (X j) ′ C .

f (Xj) az osztály hátsó valószínűségének oszlopvektora a bináris és a többosztályos osztályozáshoz. C az a költségmátrix, amelyet az input modell a Cost tulajdonságban tárolt.

J megfigyelés esetén jósolja meg a minimális várható osztályozási költségnek megfelelő osztálycímkét:

y ^ j = min j = 1,., K (γ j) .

A C segítségével azonosítsa az előrejelzéshez kapcsolódó költségeket (cj).

A súlyozott, átlagos, minimális költségveszteség

L = ∑ j = 1 n w j c j .

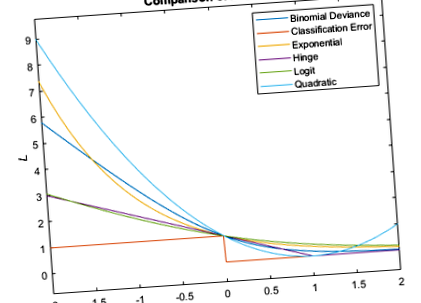
Ez az ábra összehasonlítja a veszteségfüggvényeket (kivéve a „mincost”) egy m feletti megfigyelésnél. Néhány funkció normalizálva van [0,1].

Kiterjesztett képességek

Magas tömbök
Számoljon tömbökkel, amelyeknek több sora van, mint amennyit a memóriában elférnek.

Ez a funkció teljes mértékben támogatja a magas tömböket. Ezzel a funkcióval memóriában vagy magas adatokon betanított modelleket használhat.