Statikus kerékterhelés
Kapcsolódó kifejezések:
- Vontatás
- Vasúti
- Kisiklások
- Rögzítők
- Gördülési ellenállás
- Tervezési terhelés
- Terhelhetőség
Letöltés PDF formátumban
Erről az oldalról
Súlyátadás és kerékterhelések
Absztrakt
Bevezetésre kerül a súlyátvitel fogalma. Az állandó gyorsulás esete először a gyorsítással, a fékezéssel és a kanyarodással foglalkozik. A gyorsulás nélküli statikus kerékterheléseket elkülönítik. Ezután figyelembe vesszük az alváz merevségének hatását, amely megváltoztatja a tömeg elosztási módját. Az elülső és a hátsó tömegeloszlás arányának tényezőjét vezetik be. Ezt követően mérlegelik a kombinált gyorsulás esetét, és kidolgoznak egy táblázatkezelő megoldást az általános esetre. Megmagyarázzák az átmeneti súlyátadást, és feltárják azt a tényt, hogy a súlyátvitel mind a rugózott, mind a rugózatlan tömegből származik. Tanulási projekteket, kérdéseket és irányított olvasmányokat kínálnak további tanulmányozásra.
Sínhullám *
11.4.2 Ok
A könnyű-vasúti hullámosság hullámhossz-rögzítő mechanizmusa megegyezik a nehéz szállítási hullámokéval: a jármű rugózatlan tömegének rezonanciája a pálya merevségén, elsősorban szabálytalan hegesztésekkel gerjesztve. Ebben az esetben a kritikus járműveket mozdonyként azonosították, amelyek viszonylag nagy statikus kerékterheléssel (kb. 11 tonna) és nagy rugózatlan tömeggel bírtak. 12 A károsodási mechanizmusról kiderült, hogy a sínek kihajlása a hozam, amely a sín teljes szakaszának deformációját (vagy „megnyomorítását”) okozta. Az akkor 47 kg/m és 53 kg/m sínhez használt sínacélnak viszonylag nagy szakítószilárdsága és alacsony folyási szilárdsága volt, így a műanyag hajlításhoz szükséges terhelés alacsonyabb volt, mint a mű plasztikus deformációjának előidézése. megkeményedett felületi réteg. A legtöbb acélsíntípusnál a műanyag hajlítás sokkal nagyobb terheléseknél történik, mint a műanyag áramlása. A hullámhosszak viszonylag széles tartománya a különböző sebességektől és járműtípusoktól származik: ahol ezek konzisztensek voltak, ott a hullámhosszak is konzisztensek.
A KERÉKTERHELÉS VÁLTOZÁSÁNAK OKAI ÉS HATÁSAI A MAGAS SEBESSÉGŰ MŰKÖDÉSI VONALON
5.2 A javasolt szerkezet teszt eredménye
Az újonnan javasolt pályaszerkezet tesztszakaszát 1972 szeptembere és októbere között rakták le a Tokaido Shinkansen-en. Ezt a szakaszt a 951 típusú tesztkocsi és a tömeggyártású autók felhasználásával tesztelték 1972 novemberében és decemberében. A kapott eredményeket a a következő:
A sín függőleges elmozdulása a 15. ábrán látható. Az ábra azt mutatja, hogy a pálya rugóállandó 91,2t/cm várható értéke megvalósult.
15. ábra A sín függőleges elmozdulása
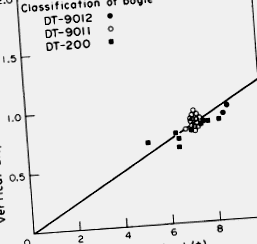
A kerékterhelés és a statikus kerékterhelés arányának szórását a 16. ábra mutatja. Az ábra azt mutatja, hogy 200 km/h sebesség alatt a javított pályaszerkezet szórása 40% -kal csökken a meglévő pályaszerkezeténél, és a 200 km/h sebesség felett a különbség a forgóváznál közel azonos DT 9011 típusú, de kisebb lesz a DT 9012 típusú forgóváz esetében.
16. ábra A dinamikus kerékterhelés és a statikus kerékterhelés eltérésének aránya (az autószerkezeti laboratórium mérésével)
A továbbfejlesztett szerkezet csökkentette a kötés, az előtét és a légszerkezet rezgésgyorsulását a meglévő szerkezetek egynegyedéről egyötödére.
A továbbfejlesztett pályaszerkezet alkalmazásával a légi szerkezet alatti zaj 8 dB (A) -kal csökkent.
A teszteket követő időszakos ellenőrzések egyértelművé teszik, hogy a továbbfejlesztett szerkezet alkalmazásával az előtét romlása jelentősen csökken.
A VASÚTI PÁLYADINAMIKA ELEMZŐ MODELLEINEK FEJLESZTÉSE
KÖVETKEZTETÉSEK
A vágányszerkezetek analitikai modelljeit lineáris elmélet alapján dolgozták ki, és a közelmúltban ezeket a modelleket használták a jármű és a pálya kölcsönhatásainak összehasonlító elemzésében, amelyek a szerkezeti paraméterek variációiból származnak. A pálya dinamikus reakciójának mérései megmutatták, hogy a modell és a tényleges szerkezet között jó a megegyezés, illetve a módosítások és finomítások szükségessé válnak. Kimondottan:
A lineáris elmélet meglehetősen jó becslést adhat a vágány teljes merevségéről (maximális kitérés egy nehéz vasúti jármű statikus kerékterhelése alatt), de az érintő rugósebesség a számított merevség 0,3 és 2,0-szerese között változhat a kerék terhelésének várható tartományában. A szimulált merevség a K r = C K P nemlineáris függvénnyel kezelhető a legjobban, ahol a CK görbeillesztési kifejezés.
A pálya csillapítása függőleges üzemmódban viszonylag magasnak tűnik, valószínűleg a pálya természetes frekvenciáján alapuló kritikus csillapítás 50–100 százaléka. A pálya csillapításának modellezésében egy lineáris hiszteretikus függvény, a pálya természetes frekvenciájára számított nagy veszteségi tényezővel, valószínűleg a legjobban megfelel a tényleges pálya impedanciának.
Annak érdekében, hogy pontos, „becsapódási” modellt kapjunk, amely szükséges a nagyobb frekvenciájú kerék-sín erők és egyéb felületi anomáliák kiszámításához, frekvenciafüggő tömegmodellt kell használni a magasan lokalizált hatások szimulálására magában a sínben. Az alacsonyabb frekvenciájú jelenségeket megfelelő módon szimulálhatjuk a folytonos sugár effektív tömegével a rugalmas alapon.
Tervezés és anyaghasznosítás
2.6 Fáradtság
A lemezanyagok viselkedése folyamatosan ingadozó stressz vagy megterhelés esetén kritikus fontosságú az élet testének szerkezete szempontjából, legyen az magas vagy alacsony frekvencia. A nagy ciklusú fáradtság jobban jellemzi a körülményeket, például a motortér közvetlen közelében, míg az alacsony ciklusú körülmények az úttest során fellépő púpok és dudorok által kiváltott körülményeket képviselik. Mindkettőt nagyon körültekintően értékelik a kezdeti mérnöki kiválasztási eljárás során, a nagy ciklusú viselkedést Wohler S – N görbékkel határozzák meg, amelyeket gyakran a CAD tervezési programok inputjaként használnak (lásd 2.22. Ábra). Az acélok általában egyértelműen meghatározott fáradási határértéket adnak, amely alatt az alkatrészek viszonylag biztonságosan megtervezhetők. Az alumínium azonban folyamatosan csökkenti a feszültséget. Az 5. fejezetben leírtak szerint óvatosan kell eljárni a hideg munkaerősítés alkalmazásával kapcsolatban - az alacsony ciklusú fáradtság fokozatos ciklikus lágyulást indukálhat, ami ellensúlyozhatja a törzs öregedése által kialakított erősítést, valamint a hideg deformációt.
2.22. ÁBRA. Fáradtsági élet értékelése: a) ciklikus stressz terminológiája; (b) S – N diagram; c) alakváltozás/élet görbék; d) dinamikus feszültség/alakváltozás görbék; e) fáradási határérték diagramok
Egy adott minta viselkedését nagyon nehéz megjósolni az anyagjellemzők jellegének és az összes testformából adódó tervezési jellemzők összetettsége miatt (ami stresszkoncentrációt eredményezhet). Ezért a kiterjedt mérések és a prediktív programok ellenére a szerkezet ciklikus viselkedésre való érzékenységének egyetlen igaz módja a rig teszt. Ez történhet egyszerű nyomás-húzás terhelés alkalmazásával, vagy kiterjeszthető a nehéz fékpálya-teszt során összegyűjtött jelek által működtetett négyplakátos szimulált mozgásokra is. A lökés-húzás próbákat, még az egyszerű szakítószilárdsági próbákat is, körültekintően kell elvégezni, hogy elkerüljük a kihajlási hatásokat, amelyek korlátozhatják a vastagság tartományát, amelyen ezeket a vizsgálatokat lehet alkalmazni. Előnyös, ha a teljes fúrótorony-szimulációhoz szükséges hidraulikus létesítményekbe lehet beruházni, mert ezek az egyetlen reális eszköz a ciklikus meghibásodásra hajlamos gyengeségek felderítésére, eltekintve természetesen a gyorsított pálya-tesztektől durva terepen.
A gyengeségeket a stresszlakk technikájának vagy hasonló alkalmazásával lehet azonosítani, és a módosítást lokalizált erősítéssel lehet végrehajtani. Az anyag tulajdonságainak hatása vitatható, mivel ismét azt állítják, hogy a test tulajdonságai ezeket cáfolják. Különösen a ponthegesztett kötések esetében sok tanulmány kimutatta, hogy nagy szilárdságú acéloknál a hegesztési geometriához kapcsolódó bevágási hatások felülmúlják az anyag szilárdságából adódó bármilyen hatást.
A fáradási folyamat és a karosszéria kialakításának ezt követő hosszabb leírása a Lightweight Electric/Hybrid Vehicle Design 5-ből származik, és tömör összefoglalást nyújt a fáradtsági ellenállást meghatározó tényezőkről, és a legtöbb testszerkezetre vonatkozik.
2.6.1 Fáradtság elleni tervezés
Dinamikus tényezőket is be kell építeni a szerkezeti terheléshez, hogy lehetővé váljon a durva utakon való haladás. Figyelembe kell venni a gyorsulás, a fékezés, a kanyarodás és a szegélyezés miatti tehetetlenségi terhelések kombinációit is. A tesztelő szervezetek jelentős közúti terhelési adatokat gyűjtöttek, és az írásos jelentéseket rögzítették MIRA és mások. A függőleges akadályt vezető két kerékre gyakorolt normál terhelések mellett figyelembe kell venni az egykerekű dudor esetét is, amely a szerkezet csavarodását okozza. Feltételezzük, hogy a szerkezetre alkalmazott nyomaték 1,5 × a statikus kerékterhelés × a tengely nyomtávjának fele. A dudor magasságától függően az egyedi statikus kerékterhelés a teljes tengelyterhelés értékéig változhat.
A fordított hajlítás fáradási határa általában körülbelül 25% -kal alacsonyabb, mint a megfordított feszültség és összenyomás esetén, állítólag a feszültséggradiens miatt - és fordított torzióban a szakítószilárdsági határérték körülbelül 0,55-szerese. A stressz megfordulásának gyakorisága szintén befolyásolja a fáradtsági határt - növekvő gyakorisággal növekszik. A Gerber miatti empirikus képlet felhasználható acélok esetében a maximális feszültség becslésére az egyes ciklusok során a fáradási határértéknél, R/2 + (σu2 - nRσu) 1/2 értékként, ahol σu a végső húzófeszültség és n értéke anyagállandó = 1,5 enyhe és 2,0 nagy szakítószilárdságú acél esetén. Ez a képlet felhasználható az enyhe acél maximális ciklikus feszültségének σ megmutatására, amely megnövekszik a fordított terhelés egyharmadánál, ismételt terhelés esetén 0,61-ig. A képlet Goodman általi átrendezése és egyszerűsítése az R = (σu/n) [1 - M/σu] lineáris összefüggést eredményezi, ahol M = σ - R/2. Az (e) nézet a fáradtságelemzés során gyakran használt Goodman vagy Gerber diagram relatív görbéit is mutatja. Ha az R és a σu értékeket fáradtsági tesztekkel találják meg, akkor a többi körülmény fáradtsági határai megtalálhatók ezen ábrákon.
Ha egy szerkezeti elem n1, n2… ciklusok sorozatára van terhelve, különböző feszültségszinteken, megfelelő fáradtsági élettartammal az N1, N2… minden egyes szintnél, a bányász törvénye szerint meghibásodásra lehet számítani failuren/N = 1 értéknél. A kísérletek azt mutatták, hogy ez a tényező 0,6 és 1,5 között változik, a növekvő terhelésű szekvenciáknál kapott magasabb értékekkel.
- Osteochondrosis - áttekintés a ScienceDirect témákról
- Rimonabant - áttekintés a ScienceDirect témákról
- Búzadara - áttekintés a ScienceDirect témákról
- Stabil angina pectoris - áttekintés a ScienceDirect témákról
- Pramlintide - áttekintés a ScienceDirect témákról