A hőveszteség kiszámítása

Mielőtt számtalan ipari hőkövetési tervbe, termékbe és alkalmazásba merülne, először meg kell értenie a hőveszteség alapjait.

A hőkövetést a folyamat hőmérsékletének fenntartására használják a csöveken, amelyeknek a környezeti hőmérsékleten megszilárduló anyagokat kell szállítaniuk, valamint a fagyvédelemre és a folyamatfolyadékok előremenő hőmérsékleten tartására. Az elektromos fűtésű és a gőzfűtéses nyomkövetést ipari hőkezelésekhez használják. A tipikus elektromos hőkövetés magában foglalja az állandó teljesítményt és az önszabályozó hőkövetést. Bár minden hőkövetés hőveszteségnek van kitéve, a hőveszteség alapjainak megértésével olyan hőkövető megoldást tervezhet, amely hatékonyan megőrzi az ipari folyamat csővezetékének hőmérsékletét.

* A cikk eredetileg a Process Heating magazin 2006. januári számában jelent meg.

Ez a cikk a hőátadás alapelveivel és a csövekhez és tartályokhoz használt számításokkal foglalkozik. Az alapvető hőátadási koncepciók megértésével felhasználhatja őket a hőveszteség-számítások során használt általános képlet eléréséhez.

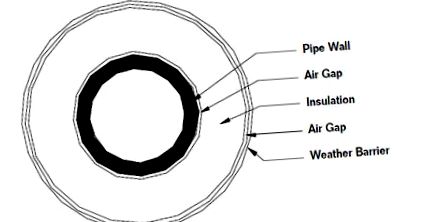
Az 1. ábra egy tipikus csőrendszer metszetét mutatja. A csőből, a szigetelésből, az időjárási akadályokból és az egyes rétegek közötti hézagokból áll. Ha a cső és annak tartalma melegebb, mint a környező környezet, akkor a hő átkerül a csőből a levegőbe. Ha elegendő hő távozik a csőből, a cső tartalma megvastagodhat vagy megszilárdulhat, ami károsíthatja a csöveket vagy a szivattyúberendezéseket.

A hő ugyanúgy áramlik egyik tárgyról a másikra, mint a víz. A termikus rendszerben az egyenlőtlen hőmérsékletű objektumok a hőegyensúly felé hajlamosak. A forróbb tárgy hőjének egy részét átadja a hidegebb tárgynak, amíg a tárgyak azonos hőmérsékletűek nem lesznek. A hő átvezethető vezetés, konvekció és sugárzás útján.

Vezetés. A vezetést úgy definiáljuk, hogy hő vagy villamos energia közvetlen közeg útján vezető közegen keresztül kerül továbbításra. A hőátadás sebessége attól függ, hogy mekkora ellenállás áll fenn a különböző hőmérsékletű tárgyak között. Sok esetben kívánatos a hő átadása egyik közegből a másikba. A főzés a tervezett hőátadás mindennapos példája. Ezenkívül a legtöbb elektronikai alkatrész hatékonyabban működik, ha a berendezés által generált felesleges hő eloszlik egy olyan közegre, amelyet a hő hozzáadása nem befolyásol hátrányosan.

Ezzel szemben a hő megőrzése egy rendszerben ugyanolyan fontos lehet, mint a hőátadás. Hideg időben a cső tartalmának fagypont felett tartása a hőátadás minimalizálásának általános gyakorlata.

Az, hogy egy anyag hővezetőként vagy szigetelőként működik-e, az anyag hőellenállási tulajdonságaitól függ. A hőellenállás (R) annak mérése, hogy egy tárgy képes-e késleltetni a hőátadást az anyag adott vastagságán keresztüli vezetés útján. Matematikailag R:

hol
L a szigetelés vastagsága hüvelykben,
k a hővezetési tényező, (BTU) (in)/(ft 2) (o F) (hr)

A vastagság (L) változásával befolyásolja a szigetelés R értékét vagy hőellenállását. A K értékek olyan állandók, amelyek specifikusak egy adott anyag fizikai tulajdonságaira. Megmérik az anyag hőátadás képességét. Néhány általános szobahőmérsékleten mért K érték az acélnál 325,300, a réznél 2750,700, az üvegszálnál 0,250 és a levegőnél 0,167.

Konvekció. A konvekció által okozott veszteségek elhanyagolhatók egy kiterjedt számítások nélküli rendszerben. Bármely csőrendszerben kis légrések vannak a felületi fal és a szigetelés között. A légrések általában kicsiek - kevesebb, mint egy hüvelyk tizede - és megakadályozzák a konvekciót korlátozó légáramlást. Bár a kis légrések nem befolyásolják a konvekció révén bekövetkező hőveszteséget, hőellenállási tulajdonságukat elemezni kell annak meghatározása érdekében, hogy a rendszer hővesztesége milyen mértékben járul hozzá a vezetéshez.

Tegyük fel, hogy az 1. ábrán látható cső 1 "üvegszálas szigetelésből áll, és a cső fala és a szigetelés közötti légrés 0,05". Az R értékegyenlet segítségével kiszámíthatja a szigetelés és a légrés ellenállását. A két ellenállás aránya azt jelzi, hogy a szigetelésnek van a legnagyobb hatása a teljes hőállóságra, és a szigetelés alkalmazásának kisebb hibái minimálisak.

A légrés miatti ellenállás százalékos aránya 0,299 osztva 4,299-vel, vagyis 6,95 százalékkal.

Sugárzás. A sugárzó hőveszteség nagy energiájú molekulák következtében hullámok vagy részecskék útján továbbítja a hőt. Ahhoz, hogy a sugárzás jelentős hőveszteséget okozzon, a forróbb felületnek jóval a környezeti hőmérséklet fölött kell lennie - sokkal magasabbnak, mint amit a tipikus hőnyomás-alkalmazásoknál megfigyelnek. Ezért a sugárzásból eredő hőveszteség figyelmen kívül hagyható.

Gyakorlati alacsony-közepes hőmérsékletű alkalmazásokban a konvekció és a sugárzás a rendszer teljes hőveszteségének körülbelül 10 százalékát teszi ki. 10 százalék hozzáadásával kiszámítható az általános képlet a rendszer hőveszteségének kiszámításához vezetés, konvekció és sugárzás útján.

Lapos felületű hőveszteség-számítások. A „hőveszteség” kifejezés általában egy tárgy hőátadására utal a környezeti környezetbe. Ez azt jelenti, hogy a kérdéses tárgy - például egy fal - a környezeti hőmérséklet feletti hőmérsékleten van (2. ábra). Matematikailag a rendszer hőveszteségének kiszámításának képlete BTU/órában kifejezve:

hol
U a vezetőképesség, BTU/(ft 2) (o F) (hr)
A az objektum felülete, ft 2
ΔT a hőmérséklet-különbség (T1 -T2), o F

A vezetőképesség az R ellenállás inverzje, és U = 1/R vagy U = k/L-ként fejezhető ki. Ezért az alap hőveszteség (Q) kifejezésének egy másik módja:

BTU-k és wattok: összehasonlítás. A fenti egyenlet egy teljes sík terület hőveszteségét számítja ki BTU/órában, de az áramot általában kilowattórában adják el. Ezért az egyenletnek konverziós tényezőre van szüksége ahhoz, hogy BTU-ból wattra konvertáljon. Egy watt 3,412 BTU. Az egyenlet módosítása új képletet eredményez:

Cső hőveszteséggel kapcsolatos szempontok ipari alkalmazásokhoz

A fenti egyenlet egy teljes sík terület hőveszteségén alapul, ahol a szigetelőfal belső területe megegyezik a külső területtel. A hőveszteség-számítás egyszerűsítése érdekében a cső hővesztesége a lineáris lábankénti hőveszteségen alapul, nem pedig az adott hosszúság teljes területén.

A csőszigetelésnél a szigetelés külső területe nagyobb, mint a belső területe, mivel a szigetelés a cső hengeres alakja köré van tekerve. Ennek eredményeként figyelembe kell venni ezt a különbséget a csövek hőveszteségének kiszámításakor.

Mivel a cső hővesztesége nem a teljes csőterületen, hanem a lineáris lábon mért watton alapul, kiszámítjuk az egy lineáris csőtalp átlagos szigetelési területét (3. ábra). Az átlagos terület (A) a külső és belső szigetelési átmérő természetes logaritmus-aránya. A cső hőveszteségének kiszámításához az alapvető hőveszteségi egyenletet (Q) a következőképpen írják át:

hol
A 2 π a henger területének kiszámításához szükséges képlet része
A 40,944 a cső 12 "-a szorozva a 3,412 konverziós tényezővel
A Do a külső szigetelés átmérője,
Di a belső szigetelés átmérője
ln (Do/Di) a szigetelés átlagos kerülete

Ez az alapvető egyenlet azonban csak a vezetésből adódó hőveszteség a csöveknél. A konvekciós és sugárzási veszteségek 10 százalékának hozzáadásával az alapvető hőveszteség-képlet végső formája:

Elsődleges vs. kiegészítő fűtés

Az elsődleges fűtés a hő hozzáadásának folyamata a rendszer hőmérsékletének emeléséhez, míg a kiegészítő fűtés csak a rendszer hőjének a jelenlegi szinten tartását szolgálja. Jellemzően az elsődleges hőhöz nagyobb hősűrűséget kell adni, szemben a kiegészítő fűtéssel. Analóg példaként vegyük figyelembe a szükséges benzinmennyiséget 0-ról 60 mph-ra gyorsuláshoz és a sebesség 60 mph-nál való fenntartásához. A gyorsuláshoz szükséges üzemanyag- és energiamennyiség sokkal nagyobb, mint a sebesség egyszerű fenntartásához szükséges üzemanyag-mennyiség.

Elsődleges hő. Az elsődleges fűtést egy anyag vagy anyagok hőmérsékletének emelésére használják. Az elsődleges fűtéshez szükséges hőmennyiség watt/órában történő kiszámításának alapképlete:

hol
m az anyag (ok) tömege (tömege)
c az anyag (ok) fajlagos hője
ΔT a szükséges hőmérséklet-növekedés
3.412 a BTU-ból wattra konvertálás

Ez a képlet használható azzal a feltétellel, hogy egyetlen anyag sem változik állapotban, azaz szilárdról folyékonyra vagy folyékonyról gázra változik. Abban az esetben, ha az anyagok állapota változik, további hőt kell adni a látens fúziós és/vagy párolgási hő befogadásához. Ha több anyagot kell melegíteni, a képlet az alábbiak szerint bővíthető.

hol
m az anyag (ok) tömege (tömege)
c az anyag (ok) fajlagos hője
ΔT a szükséges hőmérséklet-növekedés
3.412 a BTU-ból wattra konvertálás
n az anyagok száma

Minden anyag tömegét és fajlagos hőjét meg kell szorozni, majd összeadni. Az eredményt ezután megszorozzuk a hőmérséklet-emelkedéssel, végül óránként wattra konvertáljuk.

A szükséges primer hőmennyiség arányos a végső hőmérséklet eléréséhez szükséges idővel. Ha egy órás melegítéshez 10 W szükséges, akkor egy két órás melegítéshez 5 W/óra szükséges két órán keresztül. Ezzel szemben egy fél órás fűtéshez 20 W szükséges a rendszer fűtése.

Egy példa segít szemléltetni a lényeget. Tegyük fel, hogy egy 4 "-os, vízzel töltött acélcsövet egy óra alatt 40 ° F-ról (4,4 ° C) 90 ° F-ra (32 ° C) szeretne emelni. A számítást a cső egyik lábára alapozza. A mérnöki irodában található különböző táblázatokból kézikönyvek, az 1. táblázatban szereplő információkat összegyűjtjük és beillesztjük az alapvető hőegyenletbe.

Ha két óra elfogadható, akkor a cső lineáris lábánként 49,8 W/óra két órán át szolgáltatandó primer hőmennyiség.

Kiegészítő hő. A kiegészítő hő egy formálisabb kifejezés a hőveszteség-számításokra. A kiegészítő hő a meglévő hőszint fenntartásához szükséges hőmennyiség.

Szemléltetésként vegyük fontolóra ismét az acélcső példáját. Tegyük fel, hogy 1 "üvegszálas szigeteléssel szeretné kiszámítani a hőveszteség vagy a kiegészítő hőmennyiséget, amely szükséges a cső és a víz 90 ° F-on tartásához 40 ° F-os környezeti hőmérsékleten. Az üvegszál K-tényezője 0,25 BTU-in/hr-ft 2 - o F. A 4 "-es cső külső átmérője 4,5". Ezt tudjuk

A példánkban szereplő értékeket beillesztve a következőket kapjuk:

Az elsődleges és a kiegészítő hő összehasonlításához ebben a példában nyilvánvaló, hogy a kiegészítő hő alkalmazása sokkal gazdaságosabb, mivel 17,4-szer kevesebb hőt használ fel a végső hőmérséklet fenntartására, mint a hőmérséklet emelésére.

Szigetelés. A hőszigetelő rendszerben általában a szigetelés a legnagyobb ellenállókomponens. Minél jobb a szigetelési ellenállás, annál hosszabb ideig tart elérni a hőegyensúlyt. Az olyan tényezők, mint a szigetelés típusa, vastagsága és az üzemi hőmérsékleti viszonyok, befolyásolják a teljes szigetelési ellenállást.

A K tényező határozza meg a szigetelés hatékonyságát (2. táblázat). Minél alacsonyabb a K tényező, annál jobban működik szigetelőként. Ezzel szemben a magasabb K tényezőkkel történő szigetelés kevesebb hatékonyságot eredményez. Bár a K tényezőt állandó értéknek tekintjük, a K tényezőket befolyásolja a hőmérséklet. Ez annak a ténynek köszönhető, hogy a hőmérséklet növekedésével sokféle szigetelés kevésbé hatékony. Ennek eredményeként a K tényezőt átlagolják a szigetelő rétegen a fenntartási és a környezeti hőmérséklet között. Használja a következő egyenletet az átlagos K tényező meghatározásához.

Hőkövető rendszer tervezésekor ne feledje, hogy a legkisebb hőveszteséggel történő tervezés nem mindig éri el a legjobb eredményt. Például a poliuretán jobb szigetelő, mint az üvegszál, de a felső üzemi hőmérsékleti határértéke csak 200 o F. A celluláris üveg nem ugyanúgy szigetel, mint üvegszálat, de szivárgás esetén nem szívja fel a folyadékokat. Az esetek többségében azonban a szigetelés alkalmazását leginkább az üzem specifikációjára bízzák.

Ritka esetekben több réteg különböző szigetelőanyagot használnak. Amikor ez bekövetkezik, kiszámítják a rendszer teljes hőellenállását. Minden anyag ellenállását külön számítják ki, majd összegzik a rendszer teljes ellenállásában.

Hallani akarok felőled. Mondd el, hogyan tudunk fejlődni.